Question

A battery of emf 10V and internal resistance 3ohm is connected to a resistor. If the current in the resistor is 0.5A, what is the resistance of the resistor? What is the terminal voltage of the battery when the circuit is closed?

Answer 1

In order to solve this question, all we have to use is the Ohm’s law. Firstly, we have to apply the Ohm’s law in terms of the emf and the internal resistance of the battery. Then, for the closed circuit you could apply it in terms of terminal potential difference of the battery and thus find the answers accordingly.
Formula used:
Ohm’s law in terms of EMF,
$I=\dfrac{E}{R+r}$
Ohm’s law in terms of terminal voltage,
$V=I\times R$

Complete answer:
In the question, we are given a simple circuit. We have a battery of emf 10V and internal resistance 3ohm and it is further connected to a resistor of some unknown resistance R. We are also told that a current of 0.5A is measured across the resistor. With this given information, we are supposed to find the resistance of the resistor and also the terminal voltage of the battery when the given circuit is closed.

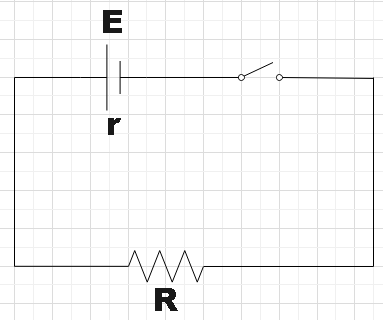
By Ohm’s law, the current in a circuit with a battery of emf E and internal resistance r and resistor of resistance R is given by,
$I=\dfrac{E}{R+r}$
$\Rightarrow R=\dfrac{E}{I}-r$
Substituting the given values into the equation, we get,
$R=\dfrac{10}{0.5}-3$
$\Rightarrow R=20-3$
$\therefore R=17\Omega$ …………………………………………… (1)
Now, when the circuit is closed, the terminal voltage is V. We could again apply Ohm’s law to get,
$V=I\times R$
$\Rightarrow V=0.5\times 17$
$\therefore V=8.5V$
Thereby, we have calculated the resistance of the resistor and also the terminal voltage V whose value is respectively given by,
$R=17\Omega$
$V=8.5V$

Note:
The electromotive force or the EMF could be defined as the terminal potential difference when no current flows through the circuit. Though both of them have the same units, that is, they are both measured in volts, they are two different concepts. The EMF could be defined as the amount of energy that is being supplied by the battery for every coulomb of charge that passes through it.