Question

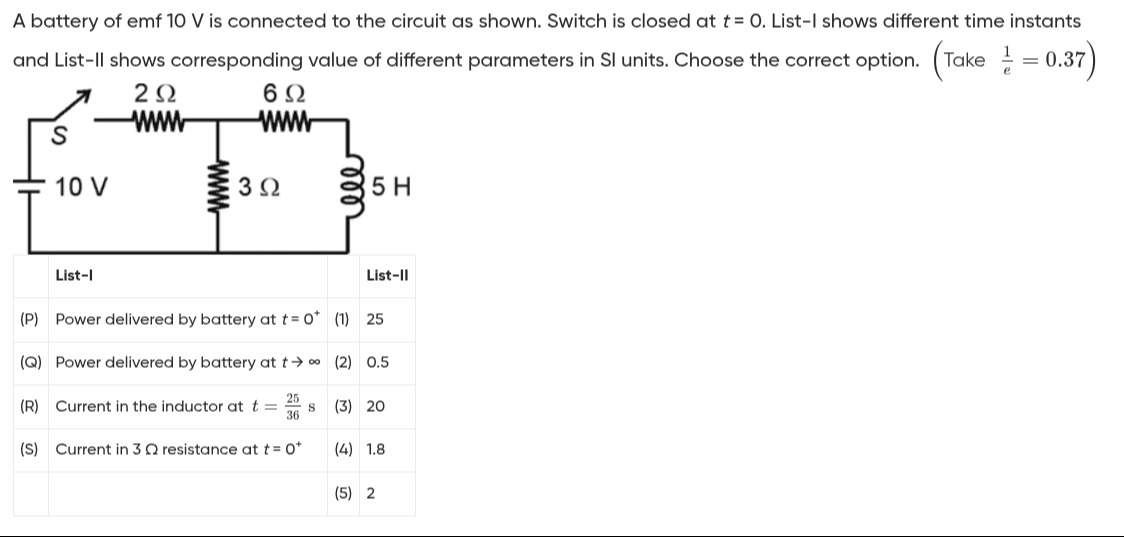
A battery of emf 10 V is connected to the circuit as shown. Switch is closed at t = 0. List-l shows different time instants and List-ll shows corresponding value of different parameters in SI units. Choose the correct option. (Take $\frac{1}{e}$ = 0.37)

[FIGURE OMITTED AS PER INSTRUCTIONS]

	List-I		List-II
(P)	Power delivered by battery at t=0$^+$	(1)	25
(Q)	Power delivered by battery at t$\rightarrow\infty$	(2)	0.5
(R)	Current in the inductor at t = $\frac{25}{36}$ s	(3)	20
(S)	Current in 3 $\Omega$ resistance at t = 0$^+$	(5)	2

• A. (P)-(3), (Q)-(1), (R)-(2), (S)-(5)
• B. (P)-(1), (Q)-(3), (R)-(5), (S)-(2)
• C. (P)-(5), (Q)-(2), (R)-(1), (S)-(3)
• D. (P)-(2), (Q)-(5), (R)-(3), (S)-(1)

Answer 1

Answer: (A)

(P)-(3), (Q)-(1), (R)-(2), (S)-(5)

Answer 2

At $t=0^+$, the inductor acts as an open circuit. The total resistance is $2 \Omega + 3 \Omega = 5 \Omega$. The total current is $I(0^+) = \frac{10V}{5\Omega} = 2A$. (P) Power delivered by battery at $t=0^+$ is $P(0^+) = 10V \times 2A = 20W$. Matches (3). (S) Current in the $3 \Omega$ resistance at $t=0^+$ is the total current, which is $2A$. Matches (5).

At $t \rightarrow \infty$, the inductor acts as a short circuit. The equivalent resistance of the parallel combination of $3 \Omega$ and $6 \Omega$ is $R_p = \frac{3 \times 6}{3+6} = 2 \Omega$. The total resistance is $2 \Omega + R_p = 2 \Omega + 2 \Omega = 4 \Omega$. The total current is $I(\infty) = \frac{10V}{4\Omega} = 2.5A$. (Q) Power delivered by battery at $t \rightarrow \infty$ is $P(\infty) = 10V \times 2.5A = 25W$. Matches (1).

The time constant of the RL circuit is $\tau = \frac{L}{R_{eq}}$, where $R_{eq}$ is the resistance seen by the inductor, which is $2 \Omega + \frac{3 \Omega \times 6 \Omega}{3 \Omega + 6 \Omega} = 4 \Omega$. So, $\tau = \frac{5H}{4\Omega} = \frac{5}{4} s$. The steady-state current through the inductor is $I_L(\infty) = \frac{V_p}{6\Omega} = \frac{I(\infty) \times R_p}{6\Omega} = \frac{2.5A \times 2\Omega}{6\Omega} = \frac{5}{6}A$. The current in the inductor at time $t$ is $I_L(t) = I_L(\infty)(1 - e^{-t/\tau}) = \frac{5}{6}(1 - e^{-t/(5/4)}) = \frac{5}{6}(1 - e^{-4t/5})$. At $t = \frac{25}{36}s$, $\frac{4t}{5} = \frac{4}{5} \times \frac{25}{36} = \frac{5}{9}$. $I_L(\frac{25}{36}) = \frac{5}{6}(1 - e^{-5/9})$. Assuming $e^{-5/9} \approx 0.4$ (which gives $I_L \approx \frac{5}{6}(1-0.4) = 0.5A$), it matches (2).