Question
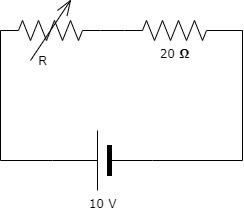
Question: A battery of 10 volt is connected to a resistance of 20 ohm through a variable resistance \(R\), the...
A battery of 10 volt is connected to a resistance of 20 ohm through a variable resistance R, the amount of charge which has passed in the circuit in 4 minutes, if the variable resistance R is increased at the rate of 5 ohm/min.
A) 120 coulomb
B) 120loge2 coulomb
C) 120/loge2 coulomb
D) 60/loge2 coulomb
Solution
The resistance prevents the free movement of the charges under a potential difference. The current flow is defined as the rate of amount of charge passed with time. This current, resistance and potential are related which need to be investigated to solve this problem.
Formulae Used:
From Ohm’s law you have
V=IR
where, V is potential difference applied, R is the resistance and I is the current flow.
Complete step by step answer:
Given: The potential of the battery is V= 10 volt.
The variable resistance is R ohm.
The rate of increase of the resistance is dtdR=5ohm/min.
The time observed is 4 min.
To get: The amount of charge passed.
Step 1:
By definition, you know that I=dtdq, where q is the total charge passed through time t.
Now express eq (1) in terms of this definition
RV=I ⇒dtdq=RV
You can represent the expression as
⇒dRdqdtdR=RV
Now you can get
dq=VdRdtRdR ⇒dq=dtdRVRdR
By the problem you have V=10 volt and dtdR=5 ohm/min.
So, finally you have
dq=60510RdR ⇒dq=120RdR
Step 2:
The observed time is 4 minutes and during that time, the variable resistance increases with the rate of
dtdR=5 ohm/min.
The total increase in resistance is
⇒dR=605dT=605×4×60 ohm =20 ohm
Calculate the final resistance
⇒Rfinal=(20+20) ohm =40 ohm
Step 3:
Now to calculate the total charge passed during that observed 4 minutes, you need to integrate eq (2).
∫dq=120∫2040RdR ⇒Q=120×[logeR]2040 ⇒Q=120×[loge40−loge20] ⇒Q=120×loge2040 ⇒Q=120×loge2
∴Q=120loge2 coulomb
If a battery of 10 volt is connected to a resistance of 20 ohm through a variable resistance R, the amount of charge which has passed in the circuit in 4 minutes, if the variable resistance R is increased at the rate of 5 ohm/min, is 120loge2 coulomb. Hence option B is correct.
Note:
Only the resistance is said to be variable. You should treat the rest terms even the rate of increase of the resistance to be constant. When the dependence of the charge and the variable is established, you should understand that a continuous relative change is happening and hence, you should attempt the integration. Be careful in choosing the limits of the resistance during the observed time.
