Question

A battery of $10\,{\text{V}}$ and negligible internal resistance is connected across the diagonally opposite corner of a cubical network consisting of ${\text{12}}$ resistors each of resistance ${\text{1}}\Omega$. The total current $I$ in the circuit external to the network is

A. $0.83\,{\text{A}}$
B. $12\,{\text{A}}$
C. $1\,{\text{A}}$
D. $4\,{\text{A}}$

Answer 1

The resistances here are neither in series nor in parallel. But there is symmetry in the circuit. Using Kirchhoff’s second law in for a closed loop, derive an equation for current in the circuit.

Complete Step by step answer: Given,
EMF of the battery $\varepsilon {\text{ = 10}}\,{\text{V}}$
Resistance of each resistor $R = 1\,{{\Omega }}$

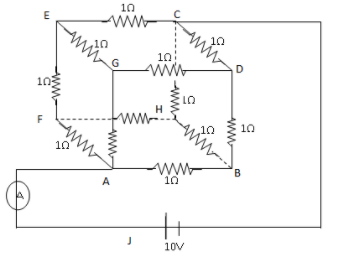
Let the total current external to the network be $3I$.
From the figure, we can see at point A, current is divided into three parts along the branch AB, AG and AF. Since the branches have equal resistance of $1\,{{\Omega }}$ so current is divided into three equal parts so each branch will have current $I$.
Again, each of the three branches AB, AG and AF, divide into two branches having equal resistance, so the current gets divided again into two equal parts, each branch having current $\dfrac{I}{2}$.
At point C, from the figure we see three branches meet having current $I$, the leaving current is also $3I$.
Now, applying Kirchhoff’s second law to the closed loop ABDCJA, we have
$- IR - \dfrac{I}{2}R - IR + 10 = 0$..................... (i)
where $- IR$ is the voltage across branch AB, $- \dfrac{I}{2}R$ is the voltage across branch BD, $- IR$ is the voltage across branch CD and the emf of the battery is ${\text{10}}\,{\text{V}}$.
Equation (i) implies,

$$\- 2IR - \dfrac{I}{2}R + 10 = 0 \\\ \Rightarrow \dfrac{5}{2}I = 10 \\\ \Rightarrow I = 4 \\\$$

The total current was taken to be $3I$, therefore total current in the circuit external to the network is $3I = 3 \times 4 = 12\,{\text{A}}$

Hence, the correct option is option (B) $12\,{\text{A}}$

Note: For problems involving such complex circuits, always try to simplify the circuit and the resistances are neither in series nor in parallel then try to look for symmetry and look for a closed loop where Kirchhoff’s law could be applied.