Question

A battery having 12V emf and internal resistance $3\Omega$ is connected to a resistor. If the current in the circuit is 1A, then the resistance of resistor and lost voltage of the battery when circuit is closed will be:
A) $7\Omega$, 7V
B) $8\Omega$, 8V
C) $9\Omega$, 9V
D) $9\Omega$, 10V

Answer 1

Voltage and current are given. So using the relation between internal resistance and emf find the resistance of an unknown resistor. Then, subtracting the total current flowing through $3\Omega$ resistor and resistance from emf will give you the lost voltage of the battery when the circuit is closed.
Formula used:
$V=IR$

Complete answer:

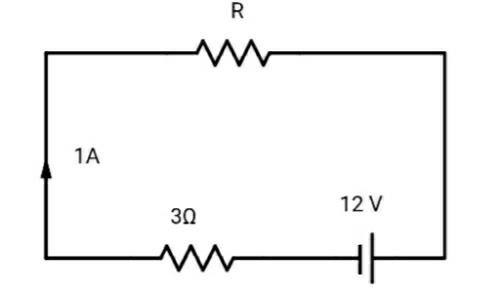
Given: Current in the circuit (I)= 1A
Internal Resistance (r)= 3$\Omega$
EMF (E) = 12V
We know the relation between internal resistance and EMF is given by,
$R= \dfrac {E-Ir}{I}$
Substituting values in above equation we get,
$R= \dfrac {12-(1 \times 3)}{1}$
$\Rightarrow R= 12-3$
$\Rightarrow R= 2\Omega$
Lost voltage of the battery= $\epsilon-Ir$
Substituting values in above equation ee get,
Lost Voltage = $12 – (3 \times I)$
$\Rightarrow Lost \quad Voltage = 12 – (3 \times 1)$
$\Rightarrow Lost \quad Voltage = 12 – 3$
$\Rightarrow Lost \quad Voltage = 9V$
Thus, the resistance of the resistor is $9\Omega$ and the lost voltage of the battery is 9V.

Hence, the correct answer is option C i.e. $9\Omega$, 9V.

Note:
- Lost voltage of the battery when circuit is closed is called the Terminal Voltage. There is an alternate method to solve this problem and find this terminal voltage.
- Using Ohm's law, this terminal voltage can also be calculated. Substituting the value of current and resistance of the resistor connected the terminal. Thus, you can calculate the lost voltage of the battery when the circuit is closed.