Question

A batsman deflects a ball at an angle ${{45}^{\centerdot }}$ without changing its initial speed which is equal to $54kmsh{{r}^{-1}}$. Mass of the ball is $0.15kg$. What is the impulse imparted to the ball.
a) $4.2kgm{{s}^{-1}}$in the direction of the final velocity
b) $4.2kgm{{s}^{-1}}$in the direction of the initial velocity
c) $4.2kgm{{s}^{-1}}$in the direction opposite to the initial velocity
d) $4.2kgm{{s}^{-1}}$directed along the bisector of the initial and the final directions of the velocity

Answer 1

Hint : Force imparted to the ball is equal to the change in momentum of the ball. If the change in momentum is positive then the impulse generated is in the direction of its initial momentum. But if the change in momentum is negative than the Impulse generated is in the direction of its final momentum

Complete solution:
Before we begin with the solution let us understand the relation between impulse and momentum.
Momentum of any body is given by,
$\overline{p}=mv$
Where m is the mass of the body and v is the velocity of its motion.
Differentiating the equation of momentum with respect to time, we get
$\dfrac{d\overline{p}}{dt}=\dfrac{dmv}{dt}$
Using law of differentiation for product,
$\dfrac{d\overline{p}}{dt}=\dfrac{vdm}{dt}+\dfrac{mdv}{dt}$
In the above case the mass of the ball does not change with time hence,
$\dfrac{dm}{dt}=0$, therefore
$\dfrac{d\overline{p}}{dt}=\dfrac{mdv}{dt}$
Now since $\dfrac{dv}{dt}$is equal to acceleration of the object dented by a,
$\dfrac{d\overline{p}}{dt}=ma$
Let us call this as equation 1
By Newton’s second law we also know,
Rate of change in momentum is equal to force acting on the body or the object.
By definition Impulse is equal i.e.$I=F\times t$
Equation 1 can also be written as,
$d\overline{p}=madt$, since $\overline{F}=ma$
$d\overline{p}=\overline{F}dt$
For $dt$sufficiently large the above equation becomes,
$\Delta \overline{p}=I$ $\Delta \overline{p}=\overline{F}\times t$
Hence from the definition of impulse,
$I=\Delta \overline{p}$

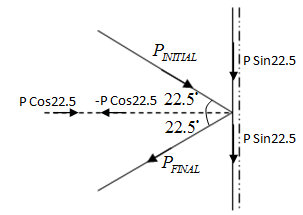
In the above diagram ${{P}_{INITIAL}}$ is the momentum of the ball before the batsman hits and deflects it to ${{45}^{\centerdot }}$and ${{P}_{FINAL}}$is the momentum of the ball after the ball has been hit.
The vertical and the horizontal components of the final and the initial momentum are resolved as shown in the figure.
Change in momentum along the vertical,
Final momentum – Initial momentum
$={{P}_{FINAL}}\operatorname{Sin}{{22.5}^{\centerdot }}-{{P}_{INITIAL}}\operatorname{Sin}{{22.5}^{\centerdot }}$
=0
Change in momentum along the horizontal,
Final momentum – Initial momentum
$=-{{P}_{FINAL}}\operatorname{Cos}{{22.5}^{\centerdot }}-{{P}_{INITIAL}}\operatorname{Cos}{{22.5}^{\centerdot }}$
Since ${{P}_{FINAL}}$and ${{P}_{INITIAL}}$are equal i.e.
$mv=0.15kg\times 15m{{s}^{-1}}=2.25kgm{{s}^{-1}}$ Conversion to SI units i.e. $54km{{h}^{-1}}=15m{{s}^{-1}}$
$=-2{{P}_{FINAL}}\operatorname{Cos}{{22.5}^{\centerdot }}kgm{{s}^{-1}}$
Substituting for ${{P}_{FINAL}}$in the above equation we get,
$=-2\times 2.25\times 0.9238795kgm{{s}^{-1}}$
$=-4.16kgm{{s}^{-1}}approx$
Negative sign indicates that the impulse imparted is away from the batsman. Hence the direction of the impulse imparted is in the direction of the final velocity.

Note:
Resolving of the momentum vector should be done using laws of vector addition. The sign convention can be done anyhow but the direction of the change in momentum will remain the same. However initial momentum of the body should be convened with a positive sign for simplicity.