Question

A barometer is faulty. When the true barometer readings are$73$ and $75$ cm of Hg, the faulty barometer reads $69{\text{cm}}$ and $70{\text{cm}}$respectively. What is the true reading when the faulty barometer reads $69.5cm?$

Answer 1

A barometer is an instrument which is used to measure atmospheric pressure and so it is also called the barometric pressure. Most of the barometers consist of the mercury which has the standardized determinations which are used to calculate the air pressure.

Complete step by step answer:

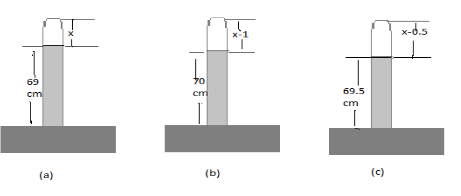
Let us consider the above three cases, where the density of the mercury be $\rho$ and the cross-sectional area of the barometer be A.
Case (a): The length of the mercury level given is $69 cm$ and let the remaining trapped air be$= x$
Case (b): The length of the mercury level given is $70 cm$ and let the remaining trapped air be$= x - 1$ (since the overall length of the barometer remains the same.
Case (c): The length of the mercury level given is $69.5 cm$ and let the remaining trapped air be$= x - 0.5$
Now, Use the formula for the pressure in barometer –
${P_0} = \rho gh + {P_1}$
At ${P_0}$ is the actual pressure.
Case (a):
Substitute the known values –
$\rho g(73) = \rho g(69) + {P_1}$
Simplify the above equation –
${P_1} = \rho g(4){\text{ }}.......{\text{(1)}}$
Case (b):
Substitute the known values –
$\rho g(75) = \rho g(70) + {P_2}$
Simplify the above equation –
${P_2} = \rho g(5){\text{ }}.......{\text{(2)}}$
Now, using the Boyle’s Law where temperature remains the constant –
Where V is the volume,
$V = A \cdot x$
$\Rightarrow {P_1}{V_1} = {P_2}{V_2}$
Place the values from the equations $(1){\text{ and (2)}}$
$\rho g(4) \times Ax = \rho g(5) \times A(x - 1)$
Take $\rho ,g{\text{ and A}}$ common from both the sides of the equation and remove them
$4x = 5(x - 1) \\\ \Rightarrow 4x = 5x - 5 \\\ \Rightarrow x = 5cm{\text{ }}......{\text{(3)}} \\\$
Case (c): Let “h” be the true pressure measured by the barometer
${V_3} = A(x - 0.5)$
Place value of “x”
${V_3} = A(4.5)$
Now, Use Boyle’s law
${P_1}{V_1} = {P_3}{V_3}$
$\Rightarrow \rho g(4) \times A(5) = {P_3} \times A(4.5)$
Remove “A” from both the sides of the equations –
${P_3} = \rho g\left( {\dfrac{{20}}{{4.5}}} \right) \\\ \Rightarrow {P_3} = \rho g(4.44) \\\$
Substitute above value in the equation $\rho gh = \rho g{h_o} + {P_3}$
${h_0} =$ Observed height
$\Rightarrow \rho gh = \rho g(69.5) + \rho g(4.44)$
Take $\rho {\text{ and g}}$ common from both the sides of the equation and remove them
$h = 69.5 + 4.44 \\\ \therefore h = 73.94cm \\\$

The true reading of the faulty barometer when the faulty barometer reads $69.5 cm$ is $73.94 cm$.

Note: Remember the basic five types of gas laws which deal with how gases behave with respect to the pressure, volume and temperature to solve these types of problems.
-Boyle’s law
-Charles’ law
-Gay-Lussac’s law
-Combined law
-Ideal Gas law
Also, remember the basic conversion relations to convert units and solve these types of problems.