Question

A bar of square cross section of side a is subjected to a tensile load P on a plane inclined at ${45^ \circ }$ to the axis of the bar, the normal stress will be:
A) $\dfrac{P}{{{a^2}}}$
B) $\dfrac{{2P}}{{{a^2}}}$
C) $\dfrac{P}{{2{a^2}}}$
D) $\dfrac{P}{{4{a^2}}}$

Answer 1

Before we try to solve for the stress, we have to understand the type of loading on the bar. In the question, it is mentioned that the loading is tensile. This means that the force acts along the axis of the body. In this case, the stress generated is known as the normal stress.

Complete step by step answer:
Stress is defined as the resistive force developed by the body per unit area due to the external loading. Mathematically, it has the same dimensions as that of pressure, which is the ratio of force per unit area. The unit of stress is also, same as that of pressure, which is pascal (Pa).
$\sigma = \dfrac{F}{A}$
Consider a bar of square cross-section of side a subject to tensile loading P as shown:

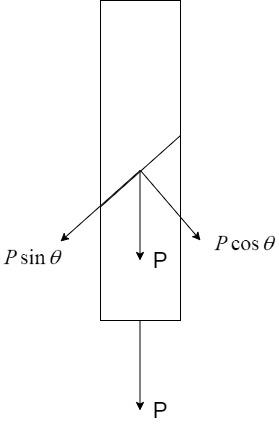
Let us consider a plane inclined at ${45^ \circ }$ as shown. The force P acting on the plane can be split into components $P\cos \theta$ and $P\sin \theta$.
The normal stress is defined as the force acting in the perpendicular direction to the plane per unit area.
The normal stress acting on the plane is given by –
$\Rightarrow {\sigma _n} = \dfrac{{P\cos \theta }}{A}$
Since the plane is at angle of ${45^ \circ }$, $\cos 45 = \dfrac{1}{{\sqrt 2 }}$
When the normal stress is applied, the direction of the stress will be along the direction of the area vector. Since the area of the plane is inclined at ${45^ \circ }$, the area acted on, by the normal stress is given by –
The area of the cross-section in the direction of P is given by –
$\Rightarrow {A_c} = A\cos \theta$
where A = area of cross-section in the direction of the plane.
So, the area of cross-section in the direction of the plane is given by –
$\Rightarrow A = \dfrac{{{A_c}}}{{\cos \theta }}$
Area of cross-section of square of side a, ${A_c} = {a^2}$
Thus, area –
$\Rightarrow A = \dfrac{{{a^2}}}{{\cos \theta }}$
Substituting in the formula for normal stress,
$\Rightarrow {\sigma _n} = \dfrac{{P\cos \theta }}{{\dfrac{{{a^2}}}{{\cos \theta }}}}$
$\Rightarrow {\sigma _n} = \dfrac{{P{{\cos }^2}\theta }}{{{a^2}}}$
Substituting the value of $\theta$,
$\Rightarrow {\sigma _n} = \dfrac{{P{{\cos }^2}45}}{{{a^2}}}$
$\Rightarrow {\sigma _n} = \dfrac{P}{{{a^2}}}\left( {\dfrac{1}{2}} \right)$
$\Rightarrow {\sigma _n} = \dfrac{P}{{2{a^2}}}$

Hence, the correct option is Option C.

Note: There is another type of stress known as shear stress, which is equal to the force acting on the cross-section per unit area, acting in the direction parallel to the area. Normally, the shear stress is equal to half of the normal stress applicable on the area of cross-section.