Question

A bar of mass $m$ is pulled by means of a thread up an inclined plane forming an angle $\alpha$ with the horizontal as shown in figure above. The coefficient of friction is equal to $k$. Find the angle $\beta$ which the thread must form with the inclined planes for the tension of the thread to be minimum.

Answer 1

Draw free body diagram of bar and then solve for the tension is equal to.
Use Newton’s second law of projection.
Formula Used: ${F_{net}} = ma$

Complete step by step answer:
First draw the free body diagram

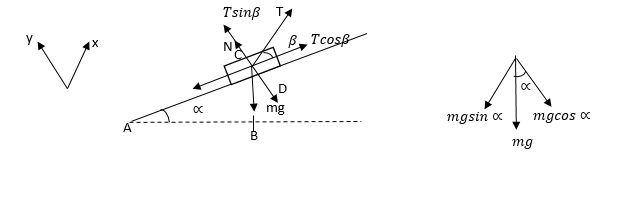
We will consider x-axis to be along the inclined plane. And Y-axis to be perpendicular to the inclined.
Let the tension on the thread be T, which is inclined at an angle of with the x-axis.
Therefore, the non-presents of T along X and Y-axis will be$T\cos \beta$and$T\sin \beta$respectively.
Normal force on the bar will be applied along the Y-axis.
Normal force is the force exerted or any object by the surface, the object is planned at. It is along perpendicular to the area of contact of the object and the surface.
One more force, that is, force due the gravity will also be applied on the bar. The force,$F = mg$will be applied downwards, as shown in the figure.
We need to resolve this force as well. For that we need to know the angle between mg and y-axis.
For that, observe,$\Delta ABC.$
$\angle CAB = \alpha .$
And clearing, $\angle Abc = 90^\circ .$
We know that the sum of angle of a triangle is equal to$180^\circ$
$\Rightarrow \angle CAB + \angle ABC + \angle ACB = 180^\circ$
$\Rightarrow \alpha + 90^\circ + \angle ACB = 180^\circ$
By rearranging it, we get
$\angle ACB = 180^\circ - 90^\circ - \alpha$
$\Rightarrow \angle ACB = 90^\circ - \alpha$
$\Rightarrow \angle BCD = \alpha$
Thus, the angle between$mg$and y-axis is$\alpha$.
Now, resolve it as$mg\cos \alpha$and$mg\sin \alpha$along positive y and x-axis, respectively.
Now, according to Newton’s second law of projection.
${F_{net}} = ma$
Where, ${F_{net}}$is the net force applied on the bar.
$m$is the mass of the bar.
$a$is the acceleration of the bar. (which is long positive x-axis).
$\therefore \sum Fx = ma$and$\sum Fy = 0$.
Where, $\sum Fx$is the net force along x-axis and $\sum Fy = 0$is the net force along y-axis.
$\Rightarrow \sum Fx = T\cos \beta - mg\sin \alpha = ma$ . . . (1)
Positive or negative sign represents the direction of the force.
And$\sum Fy = T\sin \beta + N - mg\cos \alpha$
By rearranging.
$\Rightarrow N = mg\cos \alpha - T\sin \beta$ . . . (2)
$\alpha$Now, there is one more force acting on the bar, i.e. frictional force,${f_r}$.
Frictional force is the force that is applied to oppose the motion of the object. It’s value is equal and opposite the value of the force applied.
$\therefore {f_r} = ma.$
Also,$\therefore {f_r} = kN$
Where, k is the coefficients of friction
Equation (1) becomes
$T\cos \beta - mg\sin \alpha = kN$
$\Rightarrow T\cos \beta - mg\sin \alpha - kN = 0$
Put the value of N from equation (2).
$\Rightarrow T\cos \beta - mg\sin \alpha - k(mg\cos \alpha - T\sin \beta ) = 0$
Simplifying it, we get
$T\cos \beta - mg\sin \alpha - kmg\cos \alpha + kT\sin \beta = 0$
$\Rightarrow T\cos \beta + kT\sin \beta - mg\sin \alpha - kmg\cos \alpha = 0$
$\Rightarrow T(\cos \beta + k\sin \beta ) - mg(\sin \alpha + k\cos \alpha ) = 0$
Rearranging it, we get
$T = \dfrac{{mg(\sin \alpha + k\cos \alpha )}}{{\cos \beta + k\sin \beta }}$ . . . (3)
From equation (3), we can observe that T is minimum if $\cos \beta + k\sin \beta$ is maximum.
$\Rightarrow \dfrac{d}{{d\beta }}(\cos \beta - k\sin \beta ) = 0$
$\Rightarrow - \sin \beta + k\cos \beta = 0$
Divide both the sides by$- \cos \beta$
$\Rightarrow \dfrac{{ - \sin \beta }}{{ - \cos \beta }} + \dfrac{{k\cos \beta }}{{ - \cos \beta }} = \dfrac{0}{{ - \cos \beta }}$
$\Rightarrow \tan \beta - k = 0$
$\Rightarrow \tan \beta = k$
Hence,$\beta = {\tan ^{ - 1}}(k)$for tension on the string to be minimum.

Note: Always choose x and y axis in such a way that it simplifies the question for you. Be careful while checking the angle of resolution. A small mistake will lead to the wrong answer.
Remember the concept that$\dfrac{a}{b}$is minimum when b is maximum and vice-versa.