Question

A bar magnet of dipole moment $M$ is bent at midpoint by ${90^ \circ }$(in the form of English alphabet ‘L’). The new magnetic dipole moment of the magnet will be
A. $M$
B. $\dfrac{M}{{\sqrt 2 }}$
C. $\sqrt 2 M$
D. $\dfrac{M}{2}$

Answer 1

We can find the resultant magnetic dipole moment by using the concept of magnetic dipole moment and resultant of two vectors. The dipole moment of the magnet is the product of its pole strength and its magnetic length.

Complete step by step answer:
Consider a bar magnet whose pole strength is $m$. When the bar magnet is bent at midpoint by ${90^ \circ }$, the magnetic dipole moment of each bar magnet is changed.The length of the original bar magnet is gets halved and hence, the magnetic dipole moment of each bar magnet is also gets halved as magnetic dipole moment , $M = m2l$. Here, $m$ is pole strength and $2l$ is magnetic length of the bar magnet.

Now, we know that the magnetic dipole moment is the vector quantity which directs from the South pole to North pole of the magnet. Hence, the resultant magnetic dipole moment of the new arrangement is shown as

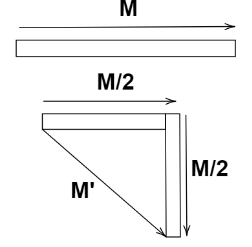
Magnitude of the resultant dipole moment is
$M' = \sqrt {{{\left( {\dfrac{M}{2}} \right)}^2} + {{\left( {\dfrac{M}{2}} \right)}^2}}$
$\Rightarrow M' = \sqrt {\dfrac{{{M^2}}}{2}}$
We get, $M' = \dfrac{M}{{\sqrt 2 }}$

So, the new magnetic dipole moment of the magnet is $M' = \dfrac{M}{{\sqrt 2 }}$.

Note: The magnetic dipole moment of the bar magnet is proportional to its length. It is a vector quantity which is directed from $- m$ to $+ m$ i.e. from south to north pole. The unit of the dipole moment is $A{m^2}$ . This is because the pole strength of the bar magnet depends on the current flowing through the area of the bar magnet.