Question

A bar magnet M is dropped so that it falls vertically through the coil C. Obtain the graph for voltage produced across the coil versus time. Explain which quantity is depicted by the area of the graph.

Answer 1

The voltage produced across the coil is proportional to the change in flux across the coil. To obtain the graph of voltage produced across the coil versus time, we need to know how the flux across the coil changes with time. Further knowing the expression the voltage produced across the coil will enable us to determine what is the significance of the area under the voltage versus time graph.
Formula used:
$E=-\dfrac{d\phi }{dt}$

Complete answer:
Let us say there is a coil and the magnetic flux across the coil changes by $d\phi$ in small time $dt$ .Than the emf (E) generated across the coil is given by,
$E=-\dfrac{d\phi }{dt}$
To obtain the graph let us say the magnet falls from some point towards the coil. As the magnet approaches the coil, the flux through the coil keeps on increasing. It is also given that the magnet is falling. Hence it will accelerate. As the velocity of the magnet keeps on increasing for every small instance of time as the magnet approaches the coil, the rate in the change of flux i.e. emf will also increase.
As soon as the magnet enters the coil, the flux across the coil will decrease and as it approaches the centre of the coil, the rate of change of flux becomes zero and within no instance of time the emf across the coil will be maximum. As the magnet leaves the coil it leaves with greater velocity than which it entered the coil. As a result, the change in flux with time i.e. emf induced across the coil will be much greater while leaving the coil. Also the flux as the coil further moves away, the emf induced will decrease at a much faster rate as the magnet moves away with greater velocity.
Hence the graph of voltage produced across the coil versus time can be traced as,

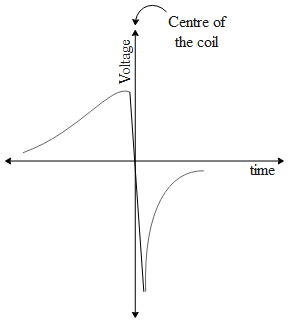
The equation of the induced emf in a coil is given by,
$E=-\dfrac{d\phi }{dt}$
For a small instance of time, the area under the curve of the above graph such that the induced emf is E during that instance is given by $Edt$ . Comparing this with the above equation we get,
$d\phi =Edt$
Hence if we integrate the area under the curve for a given time interval it will give us the flux that got linked with the coil.

Note:
The minus sign indicates that the induced emf is in the opposite direction of the increasing flux. The voltage at the center of the coil is zero and can be understood with the following analogy. As the magnet enters the coil, initially the flux that gets linked to the coil is more due to the magnet entering. As the magnet further moves into the coil, the amount of flux that gets linked with the coil due to entering is equal to that due to leaving the coil. Hence the net flux change in the coil is zero implying the voltage across the coil to be also zero.