Question

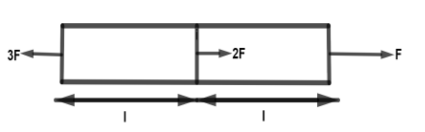
A bar is subjected to axial force as shown. If $E$ is the modulus of elasticity of the bar and $A$ is its cross-section area. Its elongation will be

A. $\dfrac{{Fl}}{{AE}}$
B. $\dfrac{{2Fl}}{{AE}}$
C. $\dfrac{{3Fl}}{{AE}}$
D. $\dfrac{{4Fl}}{{AE}}$

Answer 1

For elongation of a bar along its axial force has some modulus of elasticity and cross-section of the bar. The length of the bar is also mentioned in the diagram.There is a force $F$ on the right side of the bar and force $3F$ on the left side of the bar. In the middle of the bar the force is $2F$, and the length of the bar is $l$. From the given data we are finding the elongation of the bar.

Complete step by step answer:
From the given data, there is force, length of the bar, modulus and cross-section of the bar.Now we are going to calculate the elongation of the bar that means, $\Delta l$. For calculating the elongation of the bar we are taking the force on the right side and left side of the bar that means $F$ on the left side and $3F$ on the right side of the bar.
Then we get, $\Delta l = \dfrac{{Fl}}{{AE}}$

By adding the two forces in left and right side of the bar we can get the elongation of the bar, that means
$\Delta l = {\Delta _1} + {\Delta _3}$
Here ${\Delta _1}$ is the force on left side and ${\Delta _3}$ is the force on right side then we get
$\Delta l = \dfrac{{Fl}}{{AE}} + \dfrac{{3Fl}}{{AE}} \\\ \therefore \Delta l = \dfrac{{4Fl}}{{AE}}$
Hence we found the total elongation of the bar is $\dfrac{{4Fl}}{{AE}}$

Thus the correct option is D.

Note: In the diagram we have length of the bar, cross-section of the bar, elasticity of the bar and force on the left side, right side and middle of the bar. From this data we have taken only the right side and left side of the force for calculating the total elongation of the bar.