Question

A band playing music at frequency $1000\;{\text{Hz}}$. Is moving towards a wall at a speed of $10\;{\text{m}}{{\text{s}}^{{\text{ - 1}}}}$. A motorist is following the band with speed $5\;{\text{m}}{{\text{s}}^{ - 1}}$ frequency of reflected wave noted by motorist (in ${\text{Hz}}$ ) is (speed of sound is $330\;{\text{m}}{{\text{s}}^{ - 1}}$ ):
A) $\left[ {\dfrac{{330}}{{320}}} \right]1000$.
B) $\left[ {\dfrac{{320}}{{325}}} \right]1000$.
C) $\left[ {\dfrac{{335}}{{320}}} \right]1000$.
D) $\left[ {\dfrac{{335}}{{330}}} \right]1000$.

Answer 1

In this question, calculate the frequency of the band that plays the music by the direct source method of wave, then calculate the frequency for the direct wall. Then calculate the frequency for the reflected wave.

Complete step by step answer:
Consider the question, we are given that a band plays music at a frequency of $1000\;{\text{Hz}}$ and that is moving towards the wall at a speed of $10\;{\text{m}}{{\text{s}}^{{\text{ - 1}}}}$ and a motorist followed the band with speed of $5\;{\text{m}}{{\text{s}}^{ - 1}}$
As we know that the speed of sound by the $330\;{\text{m}}{{\text{s}}^{{\text{ - 1}}}}$, represent the speed of the motorist by the${v_m}$ and represent the band moving towards the band by ${v_b}$.
Let us consider the figure,

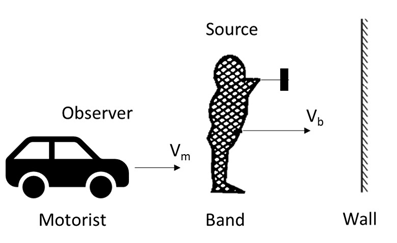
So, the motorist will listen the sound waves in two ways
$1.$Motorists will listen to the voice by the direct source.
$2.$Motorists will listen to the voice from the fixed wall.
As we know that for the direct source sound can be listen by the formula,
$\Rightarrow {f_1} = \left( {\dfrac{{v + {v_m}}}{{v + {v_{_b}}}}} \right)f$
We can also write the frequency heard by the motorist by the wall as,
$\Rightarrow {f'} = \left( {\dfrac{v}{{v - {v_{_b}}}}} \right)f$
As we can see, the direction of the wave is opposite to the motorist. So, the wave is reflected.
Now we write the expression to calculate the frequency of the reflected wave,
$\Rightarrow {f'}' = \left( {\dfrac{v}{{v - {v_{_b}}}}} \right)f = \left( {\dfrac{{v + {v_m}}}{{v - {v_{_b}}}}} \right)f$
Now, we substitute the value in the above equation as
$\Rightarrow {f'}' = \left( {\dfrac{{v + {v_m}}}{{v - {v_{_b}}}}} \right)f$
Putting the values we get,
$\Rightarrow {f'}' = \left( {\dfrac{{330 + 5}}{{330 - 10}}} \right)1000$
After simplification, we get
$\therefore {f'}' = \left( {\dfrac{{335}}{{320}}} \right)1000$

Therefore, the frequency of reflected wave noted by motorist (in${\text{Hz}}$) is (speed of sound is $330\;{\text{m}}{{\text{s}}^{ - 1}}$ ) is $\left( {\dfrac{{335}}{{320}}} \right)1000\;{\text{Hz}}$.

So, the option (C) is correct.

Note: In this solution, do not forget to write the SI unit of the frequency. Consider the speed of the sound as $v$. From the direct source and the direct wall method, we can calculate the value of the reflected wave.