Solveeit Logo
Login

Question

Question: A balloon of mass M with a light rope and monkey of mass m are at rest in mid-air. If the monkey cli...

A balloon of mass M with a light rope and monkey of mass m are at rest in mid-air. If the monkey climbs up the rope and reaches the top of the rope, the distance by which the balloon descends will be- (Total length of the rope is L)
A. mL(m+M)2\dfrac{{mL}}{{{{(m + M)}^2}}}
B. mLm+M\dfrac{{mL}}{{m + M}}
C. (m+M)Lm\dfrac{{(m + M)L}}{m}
D. (m+M)mL\dfrac{{(m + M)}}{{mL}}

Explanation

Solution

To solve this question we must have knowledge of centre of mass. For now, we can understand it as a point on or outside the body where we can say the whole mass of the system is concentrated. We already know the centre of mass of a system remains in the same state until an external force is applied. So, calculate Ycm{Y_{cm}} and in this case Ycm{Y_{cm}} will not change, apply this condition and you will get the answer.
Formula to calculate centre of mass of a body is Ycm=∑i=1nMiYi∑i=1nMiYcm = \dfrac{{\sum\nolimits_{i = 1}^n {MiYi} }}{{\sum\nolimits_{i = 1}^n {Mi} }}
Here,
Mi=Mi = Mass of ii th part
Yi=Yi = position of ii th particle from reference point.

Complete step-by-step solution:

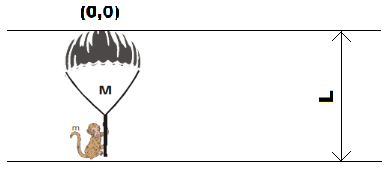
Consider the above figure with the length of rope of ‘L’ and origin at top.
Since there is no external force acting on the system, the position of Ycm{Y_{cm}} will remain the same.
So, using the above given formula Ycm=∑i=1nMiYi∑i=1nMiYcm = \dfrac{{\sum\nolimits_{i = 1}^n {MiYi} }}{{\sum\nolimits_{i = 1}^n {Mi} }}
Ycm=M×0+m×(−L)M+m{Y_{cm}} = \dfrac{{M \times 0 + m \times ( - L)}}{{M + m}}
⇒Ycm=−mLM+m\Rightarrow {Y_{cm}} = \dfrac{{ - mL}}{{M + m}}
Now, we know monkeys climbed by ‘L’ and now both masses are concentrated at the same place and a new centre of mass has been created. So, now in order to position the centre of mass at the previous place whole system will descend by mLM+m\dfrac{{mL}}{{M + m}}

Note:- This was a case of single dimension but in two or three dimensions the same calculation is performed for each to obtain coordinates of centre of mass. Newton laws of motion are also generalised for point objects. So, its generalised expressions show results for a point object or centre of mass. Calculations in mechanics are simplified when things are calculated with respect to centre of mass.