Question

A balloon of gross weight W newton descends with an acceleration$fm/{s^2}$. The weight that must be thrown out in order to give the balloon an equal upward acceleration will be.
A. $\dfrac{{Wf}}{g}$
B. $\dfrac{{2Wf}}{g}$
C. $\dfrac{{2Wf}}{{(g + f)}}$
D. $\dfrac{{W(g + f)}}{f}$

Answer 1

Initially balloon is descending with acceleration ($fm/{s^2}$.) other than acceleration due to gravity(g). That hints us that there is some other force acting on the balloon other than its weight. Since it is in air that force will be air fluid force or buoyancy force and let it be denoted by B. Now when we remove some mass(x) from the balloon it becomes lighter and starts moving up. By free body diagram and equating forces we can solve this question.

Complete step by step answer:
Initial weight be W and buoyancy force is B.
W acts in downward direction while B acts in upward direction and it is clear that W is dominating initially as the balloon is moving downward.

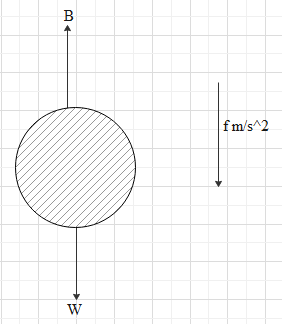
By balancing forces we get
$W - B = \dfrac{W}{g}f$ …eq 1
Where $\dfrac{W}{g}$ is initial mass before removing weight
Let us assume ‘x’ mass is removed from balloon and it started moving up with same acceleration then mass becomes $\dfrac{W}{g} - x$
Equation will be
$B - (\dfrac{W}{g} - x)g = (\dfrac{W}{g} - x)f$ …eq 2
By adding eq 1 and eq 2 we get
\eqalign{ & xg = 2\dfrac{W}{g}f - xf \cr & x(g + f) = 2\dfrac{W}{g}f \cr & x = \dfrac{{2\dfrac{W}{g}f}}{{(g + f)}} \cr}
Since they asked us to find out the weight removed we multiply mass removed with ‘g’ to get weight
So weight is
$xg = \dfrac{{2Wf}}{{(g + f)}}$

So, the correct answer is “Option C”.

Note: Generally in case of fluids it is assumed that buoyancy force is always in upward direction. But that convention is false. It is always directed from high pressure to low pressure or high force region to low force region. Here since at lower altitudes pressure is higher than higher altitude pressure buoyancy is directed upwards.