Question

A balloon is connected to a meteorological station by a cable of length$200m$, inclined at${60^ \circ }$ to the horizontal. Find the height of the balloon from the ground. Assume that there is no slack in the cable.

Answer 1

We are going to approach this problem by drawing a diagram using the given details. After we draw the diagram it is easy to proceed the problem by analysing the diagram. And then we can solve the problem using trigonometric formulae.

Formula used:

1. $\operatorname{Sin} \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Hypotenuse}}}}$
   2)$\sin {60^ \circ } = \dfrac{{\sqrt 3 }}{2}$

Complete step-by-step answer:
It is given that a balloon is connected to a meteorological station by a cable of length$200m$ and it is inclined at${60^ \circ }$ to the horizontal.
Now we are going to draw a diagram according to the given details.
At first, we are going to assume that the position of the meteorological station is at C, and the position of the balloon is B. So, BC is the cable that connects the meteorological station and the balloon.
It is given that the length of the cable is 200 m. So, ${\text{BC = 200 m}}$. And the cable BC is inclined at the angle ${60^ \circ }$to the horizontal.
Now we have all the prerequisite details to draw the diagram to the given problem. The diagram is given below.

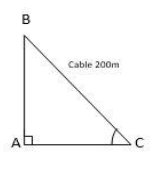
Now our aim is to find the height of the balloon from the ground. That is, we have to find the length of AB.
Now we are going to use the trigonometric formula.
We already know that, $\operatorname{Sin} \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Hypotenuse}}}}$
From the diagram, we can say that ${\text{Perpendicular = AB}}$ and ${\text{Hypotenuse = BC }}$
And we know that the length of the cable, ${\text{BC = 200 m}}$. So, ${\text{Hypotenuse = BC = 200 m}}$
Now we are going to substitute the perpendicular and Hypotenuse on$\operatorname{Sin} \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Hypotenuse}}}}$.
Hence we have that, $\sin \theta = \dfrac{{{\text{AB}}}}{{{\text{BC}}}}$.
It is given that the angle is ${60^ \circ }$. So, $\theta {\text{ = 6}}{{\text{0}}^ \circ }$
Now we are going to substitute the theta value on $\sin \theta$.
Now we have, $\sin {60^ \circ } = \dfrac{{{\text{AB}}}}{{{\text{BC}}}}$
Now we already know the value of $\sin {60^ \circ }$by trigonometric table.
Therefore, $\sin {60^ \circ } = \dfrac{{\sqrt 3 }}{2}$.
Now we are going to substitute the above value on $\sin {60^ \circ } = \dfrac{{{\text{AB}}}}{{{\text{BC}}}}$.
Hence we have,
$\dfrac{{\sqrt 3 }}{2} = \dfrac{{{\text{AB}}}}{{{\text{BC}}}}$ ........(1)
Now we have the value of the length of the cable BC is 200 m. We substitute that on the above equation. Then we get,
$\dfrac{{\sqrt 3 }}{2} = \dfrac{{{\text{AB}}}}{{200}}$
Now we want to find AB. So we are going to simplify the above equation.
Let us keep AB on one side and the remaining terms on the other side.
Then we have,
${\text{AB}} = 200 \times \dfrac{{\sqrt 3 }}{2}$
Now we are going to divide 200 by 2. Then we get,
${\text{AB}} = 100\sqrt 3$ ……(2)
We already know that the value of $\sqrt 3$ is 1.732
Now we are going to substitute the value of $\sqrt 3$ in equation (2).
${\text{AB}} = 100 \times 1.732$
On solving the above equation, we will get the height of the balloon AB.
${\text{AB = 100}} \times 1.732{\text{ = 173}}{\text{.2}}$
Therefore, ${\text{AB = 173}}{\text{.2 m}}$
Hence we finally found that the height of the balloon from the ground is ${\text{173}}{\text{.2 m}}$

Note:
We may have doubt that why we used ${\text{sin}}\theta$ to solve this problem and why we did not use other trigonometric functions like ${\text{cos}}\theta$.
If we use ${\text{cos}}\theta$ to this problem, we will have, ${\text{cos}}\theta {\text{ = }}\dfrac{{{\text{Adjacent}}}}{{{\text{Hypotenuse}}}}$. We only know the value of Hypotenuse but we don't know the value of the Adjacent side AC. So we can’t use the cosine function to solve this problem.
Also we can use ${\text{cosec}}\theta$ to this problem since ${\text{cosec}}\theta = \dfrac{1}{{{\text{sin}}\theta }}$.