Question

A balloon is ascending at the rate $v = 12{\text{km/h}}$ and is being carried horizontally by the wind at ${v_w} = 20{\text{km/h}}$. If a ballast bag is dropped from the balloon at the instant $h = 50{\text{m}}$, determine the time needed for it to strike the ground. Assume that the bag was released from the balloon with the same velocity as that of the balloon. Also, find the speed with which the bag strikes the ground.
A) $3.55{\text{s}}$ and ${\text{32}}{\text{.7m/s}}$
B) $4.55{\text{s}}$ and ${\text{40m/s}}$
C) $3.55{\text{s}}$ and ${\text{40m/s}}$
D) $4.55{\text{s}}$ and ${\text{32}}{\text{.7m/s}}$

Answer 1

The initial velocity component of the bag in the vertical direction will be the same as the velocity of the ascending balloon. The speed of the wind will be the initial velocity component of the bag in the horizontal direction. The height from the ground when the bag is dropped is the displacement of the bag in the y-direction.

Formulas used:
Newton’s first equation of motion gives the distance covered as $s = ut + \dfrac{1}{2}a{t^2}$ where $u$ is the initial velocity of the body, $a$ is its acceleration and $t$ is the time taken to cover the distance.
Newton’s second equation of motion gives the final velocity of a body as $v = u + at$ where $u$ is the initial velocity of the body, $a$ is its acceleration and $t$ is the time taken to cover the distance.
The value of $x$ in the quadratic equation $a{x^2} + bx + c = 0$ is given by the quadratic formula $x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$

Complete step by step answer:
Step 1: Sketch a rough figure describing the fall of the bag and list the parameters known from the question.

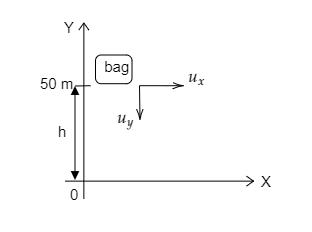
In the above figure, we see that the vertical component of the initial velocity of the bag is the same as that of the velocity of the balloon i.e., ${u_y} = 12{\text{km/h}} = 3.3{\text{m/s}}$. Also, the horizontal component of the initial velocity is the same as that of the wind velocity i.e., ${u_x} = 20{\text{km/h}} = 5.6{\text{m/s}}$ .
Since the bag is dropped when the height of the balloon is $h = 50{\text{m}}$ from the ground, the displacement of the bag in the y-direction will be ${s_y} = - 50{\text{m}}$.
The acceleration of the bag in the y-direction will be equal to the acceleration due to gravity i.e., ${a_y} = - 10{\text{m/}}{{\text{s}}^2}$. The acceleration in the x-direction is zero i.e., ${a_x} = 0$ and so the horizontal component of the final velocity will be equal to the initial horizontal velocity of the bag i.e., ${v_x} = {u_x} = 5.6{\text{m/s}}$ .
Let $t$ be the time taken by the bag to strike the ground.
Step 2: Express the equation of motion to find the time taken to reach the ground.
The distance covered by the bag as it hits the ground is given by, ${s_y} = {u_y}t + \dfrac{1}{2}{a_y}{t^2}$ -------- (1)
Substituting values for ${s_y} = - 50{\text{m}}$, ${a_y} = - 10{\text{m/}}{{\text{s}}^2}$ and ${u_y} = 3.3{\text{m/s}}$ in equation (1) we get,
$\Rightarrow - 50 = 3.3t - \dfrac{1}{2} \times 10{t^2}$
Simplifying the above equation we get,
$\Rightarrow 5{t^2} - 3.3t - 50 = 0$
The above equation is quadratic in$t$ and hence the value of $t$ is obtained by the quadratic formula, $t = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$
Substituting for $a = 5$, $b = - 3.3$ and $c = - 50$ in the given quadratic formula we get,
$\Rightarrow t = \dfrac{{3.3 \pm \sqrt {{{3.3}^2} + \left( {4 \times 5 \times 50} \right)} }}{{2 \times 5}} = 3.55{\text{s}}$
Thus the time taken for the bag to reach the ground is $t = 3.55{\text{s}}$ .
Step 3: Using Newton’s second equation of motion, we obtain the final velocity of the bag.
Newton’s second equation of motion gives the vertical component of the final velocity of the bag as ${v_y} = {u_y} + {a_y}t$ ------ (2)
Substituting values for ${u_y} = 3.3{\text{m/s}}$, ${a_y} = - 10{\text{m/}}{{\text{s}}^2}$ and $\Rightarrow t = 3.55{\text{s}}$ in equation (2) we get,
$\Rightarrow {v_y} = 3.3 - \left( {10 \times 3.5} \right) = - 32.2{\text{m/s}}$
So the vertical component of the final velocity of the bag is ${v_y} = - 32.2{\text{m/s}}$. The horizontal component of the final velocity is known to be ${v_x} = 5.6{\text{m/s}}$ .
Then the resultant velocity will be $v = \sqrt {{v_x}^2 + {v_y}^2} = \sqrt {{{5.6}^2} + {{\left( { - 32.2} \right)}^2}} = 32.7{\text{m/s}}$

Therefore the speed of the bag as it hits the ground is $v = 32.7{\text{m/s}}$. So the correct option is A.

Note:
The roots of the quadratic equation in $t$ are $t = 3.55{\text{s}}$ and $t = - 2.85{\text{s}}$ but since time cannot be negative we only consider the positive value of $t$. The acceleration of the bag along the y-direction is taken to be negative because the bag falls in the decreasing direction of the y-axis. The height of the bag also decreases as it falls down so ${s_y} = - 50{\text{m}}$.