Question

A balloon B is moving vertically upward and viewed by a telescope T. At a particular angular position $\theta = 53^\circ$. Measured parameters are $r = 1km$,$\dfrac{{dr}}{{dt}} = 3m/s$ and $\dfrac{{d\theta }}{{dt}} = 0.002rad/s$. The magnitude of the linear velocity of the balloon at this instant is:
(A) $1.2m/s$
(B) $2.4m/s$
(C) $3.6m/s$
(D) $4.8m/s$

Answer 1

Hint
When the balloon is viewed from the telescope, the r becomes hypotenuse of an imaginary triangle. The base of the triangle is the horizontal distance x from the telescope while the height of the balloon has the magnitude y. The Pythagorean equation relating all these quantities is differentiated and the value of y can be substituted in terms of r and the angle $\theta$. And then solving this equation gives us the value of $dy/dt$which is the linear velocity of the balloon at that instant.

Complete step by step answer

According to the diagram, the radial distance of the balloon from telescope r, is the hypotenuse of the triangle formed by the horizontal distance and the height of the balloon.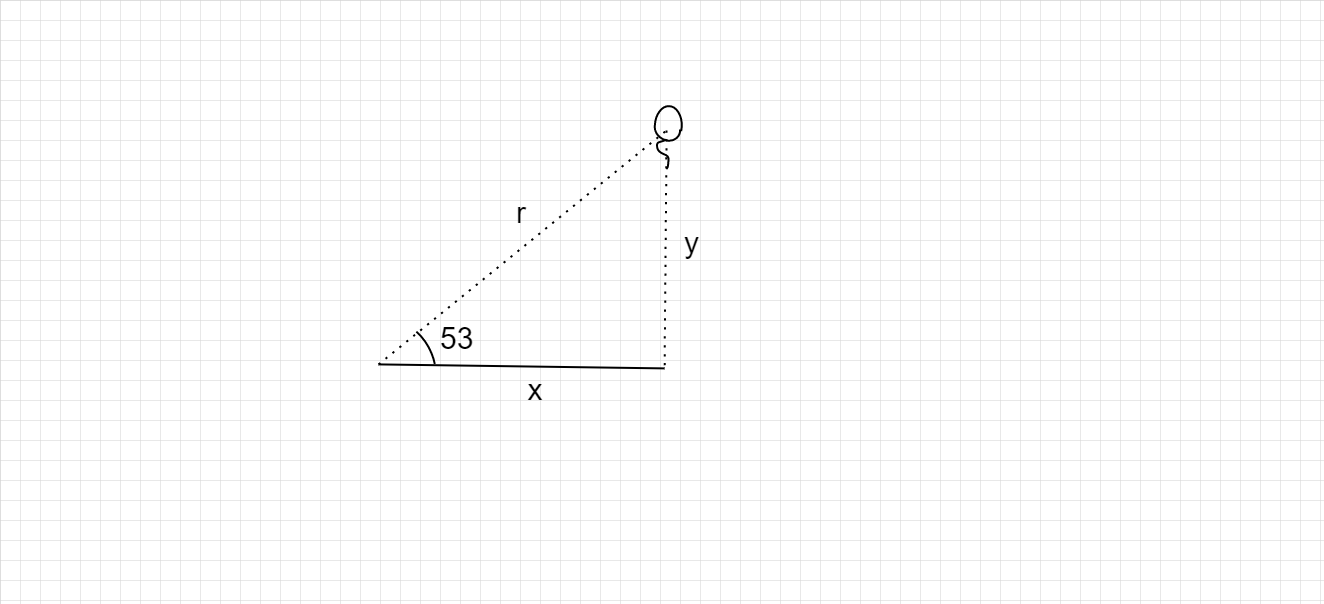
Thus Pythagoras equation for this triangle is given as-
$\Rightarrow {r^2} = {x^2} + {y^2}$
On differentiating this equation, with respect to time we get-
$\Rightarrow 2r\dfrac{{dr}}{{dt}} = 0 + 2y\dfrac{{dy}}{{dt}}$
The term ${x^2}$ becomes zero on differentiation, as it is constant.
Now we know that $y = r\sin \theta$
Therefore we can write r in terms of y and $\theta$as
$\Rightarrow y = \dfrac{4}{5}r$ (as$r = 1000$ and $\sin 53^\circ = \dfrac{4}{5}$)
On putting the value $\dfrac{{dr}}{{dt}}$and$y$, we get-
$\Rightarrow 2 \times 1000 \times 3 = 2 \times \dfrac{4}{5} \times 1000 \times \dfrac{{dy}}{{dt}}$
$\Rightarrow \dfrac{{dy}}{{dt}} = \dfrac{{5 \times 3}}{4} = \dfrac{{15}}{4} \simeq 3.6m$
Therefore option (C) is correct.
In this method of solution, the term $\dfrac{{d\theta }}{{dt}}$is not used, there can be another method to solve this with the provided information in the question, which uses this value. We use the equation,
$\Rightarrow y = r\sin \theta$
Differentiating this equation gives the terms $\dfrac{{d\theta }}{{dt}}$,$\dfrac{{dr}}{{dt}}$ and $\dfrac{{dy}}{{dt}}$ the value of r and other values are put as follows-
$\Rightarrow \dfrac{{dy}}{{dt}} = r\cos \theta \dfrac{{d\theta }}{{dt}} + \dfrac{{dr}}{{dt}}\sin \theta$
We know that$\cos 53^\circ = \dfrac{3}{5}$, $r = 1000m$
$\Rightarrow \dfrac{{dy}}{{dt}} = 1000 \times \dfrac{3}{5} \times 0.002 + 3 \times \dfrac{4}{5}$
$\Rightarrow \dfrac{{dy}}{{dt}} = 1.2 + 2.4$
$\Rightarrow \dfrac{{dy}}{{dt}} = 3.6m/s$.

Note
In the first method, the values of r and $\dfrac{{d\theta }}{{dt}}$ are not used, therefore it is ideal to solve the question with the second method in descriptive examinations, but from an objective point of view method 1 should be preferred as it has fewer calculations to perform.