Question

A ball whose kinetic energy is $E$, is thrown at an angle of ${{45}^{0}}$ with the horizontal, its kinetic energy at the highest point of its flight will be

$A)\text{ }E$ $B)\text{ }\dfrac{E}{\sqrt{2}}$ $C)\text{ }\dfrac{E}{2}$ D) zero

Answer 1

The kinetic energy of a body depends upon the square of its speed. To solve this problem we will have to find a relation between the speeds of the ball just after throwing and at the highest point of flight and using that find the kinetic energy in both the cases and calculate the required answer.

Formula used:
$KE=\dfrac{1}{2}m{{v}^{2}}$

Complete step-by-step answer:
By finding out the speeds of the ball in the two positions, we can calculate the respective kinetic energies and get the required answer. Hence, let us proceed to do that.
The path of the ball will be clearer with the help of a figure.

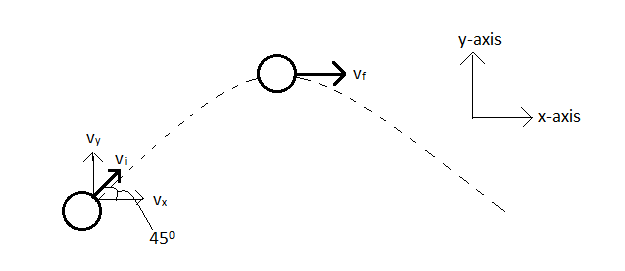
The ball follows a parabolic path. The only acceleration of the ball is in the negative y-direction, which is the acceleration due to gravity $g$.
As can be seen, at the top of the flight of the ball, the velocity of the ball is in the horizontal direction. Let this speed be ${{v}_{f}}$.
Let the magnitude of velocity of the ball just after throwing be ${{v}_{i}}$. This velocity makes an angle of ${{45}^{0}}$ with the horizontal and thus has two components, a horizontal component ${{v}_{x}}$ and a vertical component ${{v}_{y}}$.
By geometry
${{v}_{x}}={{v}_{i}}\cos {{45}^{0}}={{v}_{i}}\left( \dfrac{1}{\sqrt{2}} \right)=\dfrac{{{v}_{i}}}{\sqrt{2}}$ $\left( \because \cos {{45}^{0}}=\dfrac{1}{\sqrt{2}} \right)$ --(1)
Now, since the only acceleration of the body is in the vertically downward direction, ${{v}_{x}}$ remains unchanged. This is because, if the acceleration of a body is perpendicular to its velocity, the magnitude of the velocity is not changed.
Therefore, at the top of the flight of the ball, the speed will be nothing but the original horizontal component of the velocity of the ball just after throwing.
$\therefore {{v}_{f}}={{v}_{x}}$ --(2)
Using (1) in (2), we get,
${{v}_{f}}=\dfrac{{{v}_{i}}}{\sqrt{2}}$ --(3)
Now, the kinetic energy $KE$ of a body of mass $m$ and having speed $v$ is given by
$KE=\dfrac{1}{2}m{{v}^{2}}$ --(4)
Now, analyzing the question, we get that the kinetic energy of the ball just after throwing is $E$. Let the mass of the ball be $m$.
Therefore, using (4), we get,
$E=\dfrac{1}{2}m{{v}_{i}}^{2}$ --(5)
Now, the kinetic energy $K{{E}_{f}}$ of the ball at the top of the flight will be,
$K{{E}_{f}}=\dfrac{1}{2}m{{v}_{f}}^{2}$ [Using (4)]
$\therefore K{{E}_{f}}=\dfrac{1}{2}m{{\left( \dfrac{{{v}_{i}}}{\sqrt{2}} \right)}^{2}}=\dfrac{1}{2}m\dfrac{{{v}_{i}}^{2}}{{{\sqrt{2}}^{2}}}=\dfrac{1}{2}m\dfrac{{{v}_{i}}^{2}}{2}$ [Using (3)] $\therefore K{{E}_{f}}=\dfrac{1}{2}\left( \dfrac{1}{2}m{{v}_{i}}^{2} \right)$ $\therefore K{{E}_{f}}=\dfrac{1}{2}E$ [Using (5)]
Hence, the kinetic energy of the ball at the highest point of its flight will be $\dfrac{E}{2}$.
Hence, the correct option is $C)\text{ }\dfrac{E}{2}$.
Note: This problem could also have been solved by using the concept that the kinetic energy of a body is directly proportional to the square of the speed and hence, write the ratio of the kinetic energies of the balls in both the cases as the ratio of the squares of their respective speeds in both the cases. We would still have to find out the speeds in both the cases and a relation between them. However, using this process would take the unnecessary variable $m$ of mass of the ball out from the calculation.