Question

A ball whose density is $0.4 \times 10^3\;kgm^{-3}$ falls into water from a height $9\;cm$. To what depth does the ball sink?
A. 9 cm
B. 6 cm
C. 4.5 cm
D. 2.25 cm

Answer 1

Recall that the motion of the ball through the liquid produces a displacement of the volume of the liquid. This is brought about by contributions from the buoyant force that acts upwards against the motion of the ball. The other contributing force is the gravitational force that acts downwards. So, use a free body diagram to determine the net force acting on the ball, which in turn facilitates the acceleration of the ball through the liquid, for which you can then establish a relation from a kinematic equation of motion to determine the water depth through which the ball propagates.

Formula used:
Buoyant force exerted by a liquid at rest $F_{B} = m_{liquid}g = V\rho_{liquid} g$
Gravitational force $F_{G} = mg = \rho_{object} V$

Complete step-by-step answer:
Let us begin by first calculating the velocity with which the ball strikes the surface of water.
Since the ball is dropped from a height $h = 9\;cm$, initial velocity of the ball $u = 0$.
We have the kinematic equation: $v^2-u^2=2as$.
But since the ball falls under the influence of gravity, we have
$v^2 = 2gh \Rightarrow v = \sqrt{2gh}$
Now, when the ball enters the water, the ball experiences an upthrust, in the form of a buoyant force that impedes the velocity of the ball and consequently its motion.
Let the volume of the ball be 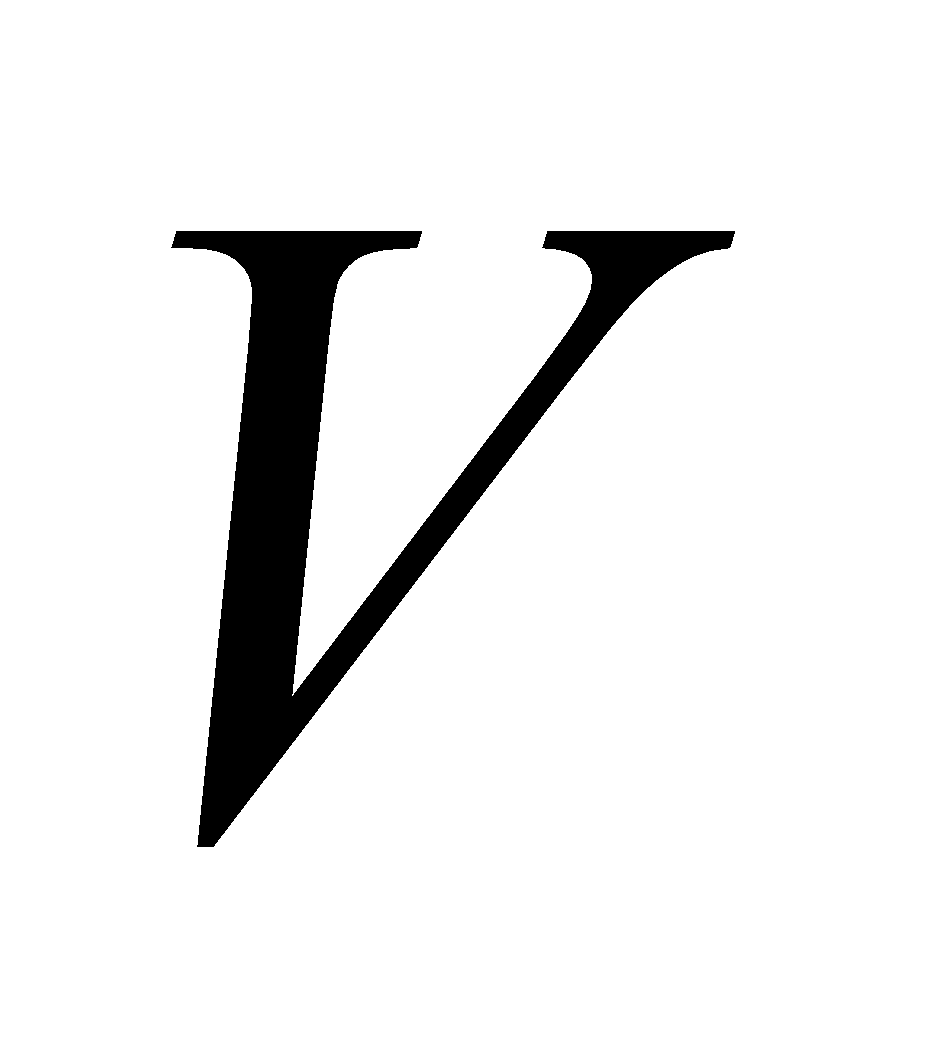. Then, the volume of water displaced by the ball as a consequence of the motion of this ball through it is also .
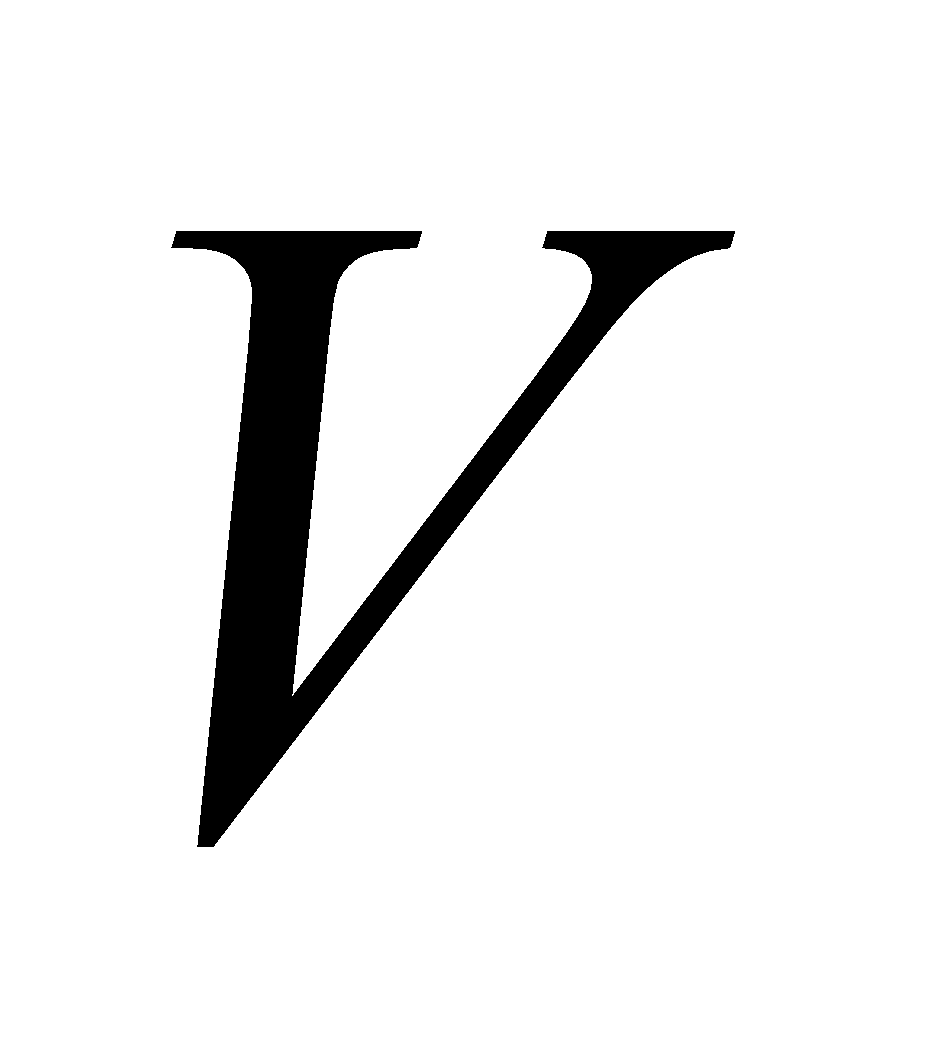Therefore, the buoyant force acting on the ball due to the water can be given as:
$F_B = m_{water}\times g = V\rho_{water}g$
The gravitational force acting on the ball due to its weight is given as:
$F_G = m_{ball} \times g = V\rho_{ball}g$
Therefore, the net force acting on the ball will be:
$F_{net} = F_G – F_B = V\rho_{ball}g - V\rho_{water}g = V(\rho_{ball}-\rho_{water})g$
Substituting $\rho_{ball} = 0.4 \times 10^3\;kgm^{-3}$ and $\rho_{water} = 1 \times 10^3\;kgm^{-3}$
$\Rightarrow F_{net} = V(0.4-1)g \times 10^3 = -0.6Vg \times 10^3\;N$

Now, the net acceleration acting on the ball will be:
$a_{net} = \dfrac{F_{net}}{m_{ball}} = \dfrac{-0.6Vg \times 10^3}{V \times 0.4 \times 10^3} = -1.5g ms^{-2}$
Assuming the depth up to which the ball will sink as S,
$u^2 – v^2 = 2a_{net} S$
$\Rightarrow 0 – 2gh = 2(-1.5g)S \Rightarrow -h =-1.5S \Rightarrow 9 = 1.5S$
$\Rightarrow S = \dfrac{9}{1.5} = 6\;cm$

So, the correct answer is “Option B”.

Note: Always use free body diagrams to summarize the list of all influencing forces in a system as this ensures that all forces are accounted for.
On a specific note, do not forget that the magnitude of buoyant force can be derived by calculating the volume of the liquid displaced, though buoyancy is a characteristic of the liquid (and not the immersed body), and is directly proportional to the density of the liquid.