Question

A ball suspended by a thread swings in a vertical plane so that its acceleration in the extreme position and lowest position are equal. The angle $\theta$ of thread deflection in the extreme position will be:
(A) ${{\tan }^{-1}}\left( 2 \right)$
(B) ${{\tan }^{-1}}\left( \sqrt{2} \right)$
(C) ${{\tan }^{-1}}\left( \dfrac{1}{2} \right)$
(D) $2{{\tan }^{-1}}\left( \dfrac{1}{2} \right)$

Answer 1

Hint : The angle of deflection can be found by equating the tangential acceleration at the extreme position with the radial or normal acceleration at the lowest position. The acceleration at the highest point is only due to gravitation, while at the lowest point it is due to the centripetal force.

Complete Step By Step Answer:
To understand the arrangement and the motion of the suspended ball, let us make a figure as shown.

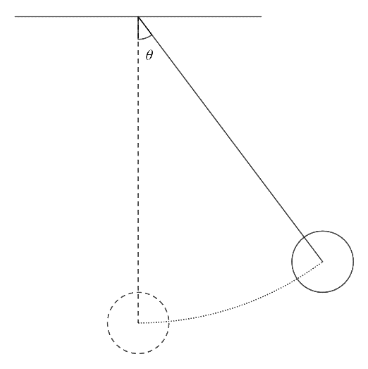
Here, we will consider the lowest point of the motion as the reference
Now, when the ball reaches the maximum height, we can say it has the highest potential energy and as the motion stops there, the kinetic energy to be zero.
Similarly, when the ball reaches the lowest point, as it is a reference point, the potential energy can be said to be zero and as the ball tends to move towards height, kinetic energy is maximum.
Now, from the law of conservation of energy, we can say that the total energy at the height is equal to the total energy at the base or reference.
${{E}_{h}}={{E}_{b}}$
$\therefore K{{E}_{h}}+P{{E}_{h}}=K{{E}_{b}}+P{{E}_{b}}$
Substituting the known values,
$\therefore 0+P{{E}_{h}}=K{{E}_{b}}+0$
$\therefore P{{E}_{h}}=K{{E}_{b}}$ …… $(1)$
Now, let us suppose the length of the thread as $l$ .
Now, for the acceleration at the highest position, we know at the extreme position, the force acting is only due to the gravitational force. But as the gravitational force acts in the downward direction, we need to consider the component of the force in the direction of the motion as shown in the figure below

Hence, the force acting at the extreme position is
${{F}_{h}}=mg\sin \theta$
Hence, the acceleration can be expressed as,
${{a}_{h}}=g\sin \theta$ …… $(2)$
For the acceleration at the lowest position, we know that the acceleration to reach extreme height is provided by the centripetal force,
${{F}_{b}}=\dfrac{m{{v}^{2}}}{l}$
Hence, the acceleration can be expressed as,
${{a}_{b}}=\dfrac{{{v}^{2}}}{l}$ …… $(3)$
Now, for the equation $(1)$ , we can write
$\therefore mgh=\dfrac{1}{2}m{{v}^{2}}$
The height of the ball at the extreme position from the geometry of the figure can be expressed as $h=l-l\cos \theta$
Substituting the value,
$\therefore mg(l-l\cos \theta )=\dfrac{1}{2}m{{v}^{2}}$
Canceling the common terms, and taking common terms out of parenthesis
$\therefore gl(1-\cos \theta )=\dfrac{1}{2}{{v}^{2}}$
Rearranging the equation,
$\therefore 2g(1-\cos \theta )=\dfrac{{{v}^{2}}}{l}$
From the equation $(3)$ ,
$\therefore 2g(1-\cos \theta )={{a}_{b}}$
But, we are given that the acceleration at the base is equal to acceleration at the extreme position.
$\therefore 2g(1-\cos \theta )={{a}_{h}}$
From the equation $(2)$ ,
$\therefore 2g(1-\cos \theta )=g\sin \theta$
Now, we know the expansions for the trigonometric terms as,
$\sin 2\theta =2\sin \theta \cos \theta$ and $\cos 2\theta =1-2{{\sin }^{2}}\theta$
Applying the trigonometric expansions,
$\therefore 2g\times 2{{\sin }^{2}}\dfrac{\theta }{2}=g\times 2\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}$
Canceling the common terms,
$\therefore 2\sin \dfrac{\theta }{2}=\cos \dfrac{\theta }{2}$
$\therefore \tan \dfrac{\theta }{2}=\dfrac{1}{2}$
Applying the inverse functions,
$\therefore \dfrac{\theta }{2}={{\tan }^{-1}}\dfrac{1}{2}$
$\therefore \theta =2{{\tan }^{-1}}\dfrac{1}{2}$
Hence, the correct answer is Option $(D)$ .

Note :
At the highest point, the potential energy is the highest and the kinetic energy is zero and the acceleration is always towards the lowest point acting tangentially. While at the lowest point, the kinetic energy is the highest and the potential energy is zero and the acceleration is towards the highest point due to the centripetal force acting tangentially. The normal acceleration does not affect the motion.