Question

A ball rolls off the top of a stairway with horizontal velocity ${{v}_{0}}\,m{{s}^{-1}}$. If the stairs are $h$ metres high and $w$ metres wide, the ball will hit the edge of ${{n}^{th}}$ step, if
(A). $n=\dfrac{2h{{v}_{0}}}{g{{w}^{2}}}$
(B). $n=2h\dfrac{v_{0}^{2}}{gw}$
(C). $n=\dfrac{hv_{0}^{2}}{g{{w}^{2}}}$
(D). $n=\dfrac{2hv_{0}^{2}}{g{{w}^{2}}}$

Answer 1

The ball follows projectile motion down a stairway and stops when it hits the ${{n}^{th}}$ stair. The distance covered by it in vertical direction will be $nh$ and the distance covered horizontally will be $nw$. We can use the properties of a projectile motion to determine the value of $n$.

Formulas used:
$y=x\tan \theta -\dfrac{g{{x}^{2}}}{v_{0}^{2}{{\cos }^{2}}\theta }$

Complete step-by-step solution:

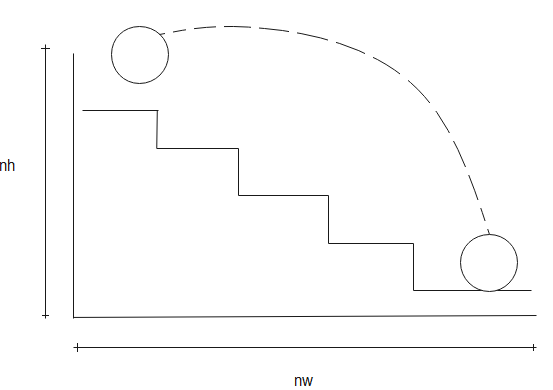
The ball follows a projectile motion down the stairway. If the height of one stairway is $h$ metres, then the total height travelled by the ball will be $nh$ metres ($n$ is the number of steps the ball travels down). Similarly, the horizontal distance travelled by the ball will be $nw$ metres.

We know the equation of trajectory in a projectile motion is given by-
$y=x\tan \theta -\dfrac{g{{x}^{2}}}{v_{0}^{2}{{\cos }^{2}}\theta }$
Here,
$y$ is the distance travelled along the y-axis
$x$ is the distance travelled along the x-axis
$g$ is acceleration due to gravity
$\theta$ is the angle made by the trajectory
At the point where the ball strikes the ${{n}^{th}}$ step, $\theta =0$

We substitute given values in above equation to get,
$\begin{aligned} & nh=nw\tan 0-\dfrac{g{{(nw)}^{2}}}{v_{0}^{2}{{\cos }^{2}}0} \\\ & \Rightarrow nh=\dfrac{g{{n}^{2}}{{w}^{2}}}{v_{0}^{2}} \\\ & \therefore n=\dfrac{v_{0}^{2}h}{g{{w}^{2}}} \\\ \end{aligned}$

Therefore, the value of n where the ball hits the step is $\dfrac{v_{0}^{2}h}{g{{w}^{2}}}$. Hence, the correct option is (C).

Additional Information:
In order to study projectile motion, we break into two motions along x-axis and y-axis which are independent of each other. We can apply the equations of motion in both directions separately and calculate various parameters like total height covered, $h=\dfrac{v_{0}^{2}}{2g}$, range; $R=\dfrac{v_{0}^{2}\sin 2\theta }{g}$ etc.

Note:
When an object follows projectile motion, it covers distance in x-axis as well as y-axis, it moves in a parabolic path. The velocity is resolves in both directions; velocity against x-axis remains constant throughout the trajectory. At the highest point of trajectory, the velocity is zero. While at the lowest point, the velocity is maximum.