Question

A ball P moving with a speed of v ms-1 collides with another identical ball Q moving with a speed 10ms-1 in the opposite direction. P comes to rest after the collision. If the coefficient of restitution is 0.6, the value of v is:
A) 30ms-1
B) 40ms-1
C) 50ms-1
D) 60ms-1

Answer 1

This question can be solved by using the concept of conservation of momentum by using proper sign convention.
The coefficient of restitution is the ratio of the final to initial relative velocity between two objects after the collision.

Complete step by step answer:
Two balls P and Q are moving in a direction opposite to each other. Let the velocity of P is v ms-1 and velocity of Q is $10ms^{-1}$. These two balls P and Q are identical balls; they mean both are having the same mass. P will come to rest after the collision. The coefficient of restitution is e=0.6. The coefficient of restitution is the ratio of the final to initial relative velocity between two objects after the collision.
Let us understand by drawing a diagram as follows before collision and after collision.
Before collision:

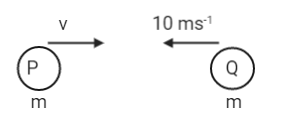
After collision:

As per law of conservation of momentum, initial momentum equals to final momentum. $P_i=P_f$ –(i)
The initial and final momentum are given by
$P_i=\left(mv\right)_P-\left(mv\right)_Q$ (negative sign is due as both are opposite in direction.
$P_f=\left(mv\right)_P+\left(mv_1\right)_Q$
Now, substitute the same in equation (i)
$\left(mv\right)_P-\left(mv\right)_Q=\left(mv\right)_P+\left(mv_1\right)_Q$ Since P and Q are identical, we cancel the term m on both sides.
$\left(v\right)_P-\left(v\right)_Q=\left(v\right)_P+\left(v_1\right)_Q$ After substituting the given values in the equation,
v-10=v_1 ------ (ii)
The coefficient of restitution is given by the ratio of the final momentum to initial momentum.
$e=\dfrac{v_1}{v-\left(-10\right)}$
$\implies$ 0.6=\dfrac{v_1}{v+10}
By cross multiplication,
$0.6\left(v+10\right)=v_1$
$\implies$ 0.6v+6=v_1 ------(iii)
Substituting equation (iii) in (i)
v-10=0.6v+6
$\implies$ v-0.6v=6+10
$\implies$ 0.4v=16
$\therefore$ $v=\dfrac{16}{0.4}=40ms^{-1}$
Hence, option B is the correct answer.

So, the correct answer is “Option B”.

Note:
Coefficient of restitution varies from 0 to 1 where 1 would be a perfectly elastic collision. Actually, for a perfectly inelastic collision coefficient of restitution is zero, which is not possible in general.