Question

A ball of mass $m$ with charge $q$ can rotate in a vertical plane at the end of a string of length $l$ in a uniform electrostatic field whose lines of force are directed upwards. Find the horizontal velocity that must be imparted to the ball in the uppermost position so that the tension in the string in the lowermost position of the ball is 15 times the weight of the ball.

Answer 1

Here, the forces present in the given system will be the force due to gravity, the electrostatic force, the centripetal force and the tension in the string. The ball will have different velocities at the top-most position and at its bottom-most position. The work-energy theorem gives the change in kinetic energy as the work done by the external forces.

Formulas used:
The change in kinetic energy of a moving body is given by, $\Delta KE = \dfrac{1}{2}m{\left( {{v_2} - {v_1}} \right)^2}$ where $m$ is the mass of the body and ${v_1}$ , ${v_2}$ are its velocities.
The electrostatic force is given by, $F = qE$ where $q$ is the charge and $E$ is the electric field present.
The work done by the electrostatic force is given by, ${W_{ele}} = F \cdot d$ where $F$ is the electrostatic force and $d$ is the displacement of the charge $q$ .
The centripetal force of a rotating body is given by, ${F_c} = \dfrac{{m{v^2}}}{r}$ where $m$ is the mass of the body, $v$ is its velocity and $r$ is the radius of the circle.

Complete step by step answer.
Step 1: Sketch a figure depicting the rotation of the ball and the various forces in play.

 ![](https://www.vedantu.com/question-sets/9f92f3f8-a8fa-4f52-9b28-4b65edc58d93935326151788871938.png)  

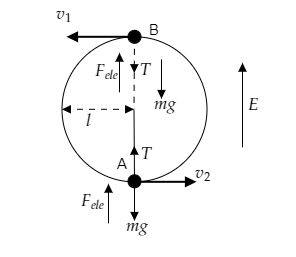
The ball tied at one end of the string of length $l$, has a charge $q$and mass $m$ and it rotates in a circle of radius.
In the above figure, the bottom-most position of the ball corresponds to the point A and the top-most position corresponds to the point B on the circle.
At A, the tension $T$ in the string is directed upwards while at B, the tension is directed downwards.
The electrostatic force ${F_{ele}} = qE$ is directed upwards at A and at B.
The weight of the ball ${F_g} = W = mg$ will be directed downwards at both A and B.
Let ${v_1}$ be the horizontal velocity of the ball at B and ${v_2}$ be the horizontal velocity of the ball at A so that the tension in the string is $T = 15mg$ at A.
Step 2: Express the force equation at A.
At A, the forces in play are the weight of the ball, electrostatic force, centripetal force and tension in the string.
At A the centripetal force of the ball will be ${F_c} = \dfrac{{m{v_2}^2}}{l}$
Then the force equation is given by, ${F_{ele}} + T - W = {F_c}$ or on substituting the respective relation for each force we have $qE + 15mg - mg = \dfrac{{m{v_2}^2}}{l}$
$\Rightarrow {v_2}^2 = \dfrac{{qEl}}{m} + 14gl$ ------- (1)
Step 3: Use the work-energy theorem to obtain an expression for ${v_1}$ .
According to the work-energy theorem, the change in kinetic energy will be the sum of the work done by the force due to gravity and the work done by the electrostatic force.
$\Rightarrow \Delta KE = {W_g} + {W_{ele}}$ --------- (2)
The work done by the force due to gravity will be ${W_g} = {F_g} \cdot d = mg\left( {2l} \right)$ .
The work done by the electrostatic force will be ${W_{ele}} = {F_{ele}} \cdot d = - qE\left( {2l} \right)$ .
The change in kinetic energy is expressed as $\Delta KE = \dfrac{1}{2}m{\left( {{v_2} - {v_1}} \right)^2}$ .
Then equation (2) becomes $\dfrac{1}{2}m{\left( {{v_2} - {v_1}} \right)^2} = 2mgl - 2qEl$
On simplifying the above equation becomes ${v_2}^2 = {v_1}^2 + 4gl - \dfrac{{4qEl}}{m}$ --------- (3)
Substituting equation (1) in (3) we get, $\dfrac{{qEl}}{m} + 14gl = {v_1}^2 + 4gl - \dfrac{{4qEl}}{m}$
$\Rightarrow {v_1}^2 = 10gl + \dfrac{{5qEl}}{m} = \dfrac{{5l}}{m}\left( {2mg + qE} \right)$
So we have the velocity at the top-most position as ${v_1} = \sqrt {\dfrac{{5l}}{m}\left( {2mg + qE} \right)}$ .

Note: The electrostatic force will be directed along the field lines. The length of the string will constitute the radius of the circle described by the ball. Then the displacement of the ball or charge at the uppermost position will be twice that of the radius of the circle i.e., $d = 2l$ . The displacement will be opposite in direction to the electrostatic force but has the same direction as that of the force due to gravity.