Question

A ball of mass M strikes another ball of mass m at rest. If they separate in mutually perpendicular directions their coefficient of impact$e=\dfrac{2\alpha M}{25m}$ .Calculate $\alpha$.

Answer 1

Recall the expression for coefficient of impact and depending on the given conditions you could substitute the required quantities. Now, apply the law of conservation of momentum along the line of impact. Using these expressions and also the given expression given in the question, you could find the value of$\alpha$.

Formula Used:
Expression for coefficient of impact,
$e=\dfrac{{{v}_{1}}-{{v}_{2}}}{{{u}_{1}}-{{u}_{2}}}$

Complete step by step answer:
In the question, we are given two balls, one of mass M and other of mass m. The ball with mass M hits the ball with mass m when the ball with mass m is at rest and after that they are separated in perpendicular directions. We are also given the expression for coefficient of impact e.
We know that the ratio of final to initial relative velocity between two objects after their collision is called coefficient of restitution or coefficient of impact (e). Its value ranges from 0 to 1.
Let ${{u}_{1}}$ and ${{u}_{2}}$ be the velocities before collision, ${{v}_{1}}$ and ${{v}_{2}}$ be the velocities after collision of two bodies, then,
Relative velocity after collision = ${{v}_{1}}-{{v}_{2}}$……………………………….. (1)
Relative velocity before collision = ${{u}_{1}}-{{u}_{2}}$ ……………………………. (2)
Then, the coefficient of impact is given by, the ratio of (1) and (2).
$e=\dfrac{{{v}_{1}}-{{v}_{2}}}{{{u}_{1}}-{{u}_{2}}}$ ……………………………… (3)
But we should note here that e is valid only along the line of impact.

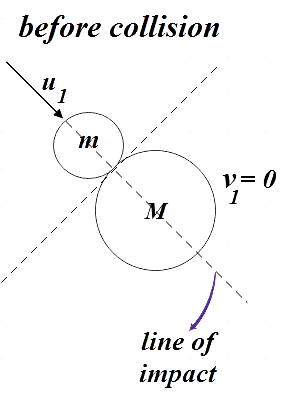
Since M is at rest and m is having a velocity of u, the relative velocities along the line of impact before collision is given by,
${{u}_{1}}-{{u}_{2}}={{u}_{1}}-0={{u}_{1}}$ …………………………. (4)

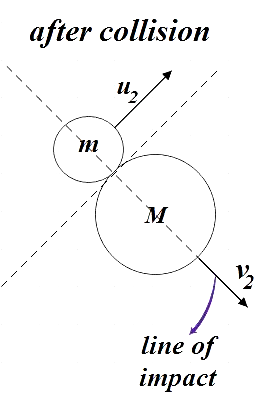
After collision both bodies are moving in direction perpendicular to each other, so, along the line of impact we have their relative velocities along the line of impact =${{v}_{2}}$
Equation (3) now becomes,
$e=\dfrac{{{v}_{2}}}{{{u}_{1}}}$………………………… (5)
In the question we are given e as,
$e=\dfrac{2\alpha M}{25m}$ ……………………… (6)
Equating (5) and (6) we get,
$\Rightarrow \dfrac{{{v}_{2}}}{{{u}_{1}}}=\dfrac{2\alpha M}{25m}$ …………………… (7)
Also applying the law of momentum conservation along the line of impact we have,
$m{{u}_{1}}=M{{v}_{2}}$
$\Rightarrow \dfrac{{{v}_{2}}}{{{u}_{1}}}=\dfrac{m}{M}$ ………………….. (8)
Substituting (8) in (7) we get,
$\Rightarrow \dfrac{m}{M}=\dfrac{2\alpha M}{25m}$
$\Rightarrow \alpha =\dfrac{25{{m}^{2}}}{2{{M}^{2}}}=12.5{{\left( \dfrac{m}{M} \right)}^{2}}$

Therefore, we get the value of $\alpha$ as $12.5{{\left( \dfrac{m}{M} \right)}^{2}}$.

Note:
We know that, normally the range of values for e varies from 0 to 1. But the value of e is significant in determining the type of collision. If the value of e=0, the collision is said to be a perfectly inelastic collision. When,$0\langle e\langle 1$ it is the case for the real-world inelastic collision. When e=1, it is a perfectly elastic collision.