Question

A ball of mass m moving with a certain velocity collides against a stationary ball of mass m. The two balls stick together during a collision. If E be the initial kinetic energy, then the loss of the kinetic energy in the collision is
$A.\,E$
$B.\,\dfrac{E}{2}$
$C.\,\dfrac{E}{3}$
$D.\,\dfrac{E}{4}$

Answer 1

This is a question based on the concept of the collision. Using the formula for computing the law of conservation of the mass we will solve this problem. We will find the value of the final kinetic energy, then, we will find the loss of the kinetic energy by subtracting the initial kinetic energy from the final kinetic energy.
Formula used:
$E=\dfrac{1}{2}m{{v}^{2}}$

Complete answer:
From the data, we have the data as follows.
A ball of mass m moving with a certain velocity collides against a stationary ball of mass m.
Therefore, the masses of both the balls are the same, that is, ‘m’.
The two balls stick together during a collision.
This implies that the final kinetic energy will be calculated as the sum of the masses.
The initial kinetic energy is given by E.

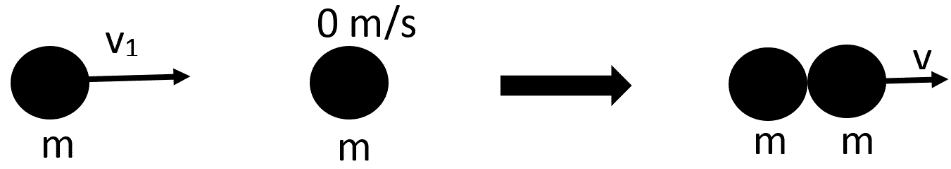
Using the law of conservation of the mass, we have the expression as follows.
${{m}_{1}}{{v}_{1}}=({{m}_{1}}+{{m}_{2}})v$
The above equation represents that the initial momentum equals the final momentum.
The initial mass and velocity are given as follows.
${{m}_{1}}=m$ and ${{v}_{1}}$
The final mass and velocity are given as follows.
${{m}_{1}}+{{m}_{2}}=m+m=2m$ and

& {{v}_{2}}=\dfrac{m{{v}_{1}}}{{{m}_{1}}+{{m}_{2}}} \\\ & {{v}_{2}}=\dfrac{m{{v}_{1}}}{2m} \\\ & \Rightarrow {{v}_{2}}=\dfrac{{{v}_{1}}}{2} \\\ \end{aligned}$$ Continue the further calculation. The initial kinetic is given by the moving ball, that is, $${{E}_{1}}=\dfrac{1}{2}mv_{1}^{2}$$ The initial kinetic is given by the system of the moving ball and the stationary ball, that is, $${{E}_{2}}=\dfrac{1}{2}({{m}_{1}}+{{m}_{2}})v_{2}^{2}$$ Substitute the values of the masses and their velocities. So, we get, $$\begin{aligned} & {{E}_{2}}=\dfrac{1}{2}(m+m){{\left( \dfrac{{{v}_{1}}}{2} \right)}^{2}} \\\ & {{E}_{2}}=\dfrac{1}{2}(2m)\left( \dfrac{v_{1}^{2}}{4} \right) \\\ & \Rightarrow {{E}_{2}}=\dfrac{mv_{1}^{2}}{4} \\\ \end{aligned}$$ Now, we will compute the loss of the kinetic energy. The loss of kinetic energy equals the difference between the initial and the final kinetic energies. $$\text{loss}={{E}_{1}}-{{E}_{2}}$$ Substitute the values of the initial and final energies. So, we get, $$\begin{aligned} & \text{loss}={{E}_{1}}-{{E}_{2}} \\\ & \text{loss}=\dfrac{1}{2}mv_{1}^{2}-\dfrac{mv_{1}^{2}}{4} \\\ & \Rightarrow \text{loss}=\dfrac{mv_{1}^{2}}{4} \\\ \end{aligned}$$ This loss value equals half the value of the initial kinetic energy, that is, $$\text{loss}=\dfrac{E}{2}$$ $$\therefore $$ The value of the loss of the kinetic energy in the collision is $$\dfrac{E}{2}$$. **As the value of the loss of the kinetic energy in the collision is $$\dfrac{E}{2}$$, thus, the option (B) is correct.** **Note:** The method of finding the final velocity should be known to solve this type of problems, in this case, as the masses were in contact, thus, we have added the masses. From the given question statement, the condition using which the problem can be solved should be known, as in this case, the condition was given to be, “conservation of the mass”.