Question

A ball of mass $M$ is thrown upward if the air resistance is considered constant ($R$). What will be times of ascent and descent? Give mathematical proof.

Answer 1

Calculate the net acceleration of the ball in the presence of constant air resistance. Use the kinematic expressions relating displacement, initial velocity, final velocity, acceleration and time.

Formulae used:
The expression for Newton’s second law of motion is
$\Rightarrow {F_{net}} = Ma$ …… (1)
Here, ${F_{net}}$ is the net force on the object, $M$ is the mass of the object and $a$ is the acceleration of the object.
The kinematic expression relating initial velocity $u$, final velocity $v$, acceleration $a$ and displacement $s$ in a free fall is
$\Rightarrow {v^2} = {u^2} - 2as$ …… (2)
The kinematic expression relating displacement $s$, initial velocity $u$, time $t$ and acceleration $a$ in a free fall is
$\Rightarrow s = ut - \dfrac{1}{2}a{t^2}$ …… (3)

Complete step by step answer:
Calculate the time of ascent of the ball while going upward.Calculate the net acceleration ${a_1}$ on the ball when thrown upward.

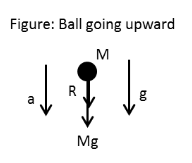
When the ball of mass $M$ is going upward, the weight of the ball and the air resistance acts in downward direction.
Apply Newton’s second law to the ball.
$\Rightarrow - R - Mg = - M{a_1}$
$\Rightarrow {a_1} = g + \dfrac{R}{M}$
Hence, net acceleration on the ball going upward is $g + \dfrac{R}{M}$.
The final velocity of the ball when it reaches its maximum height is zero.
Let ${u_1}$ and ${v_1}$ are the initial and final velocities of the ball while going upward and rewrite equation (2).
$\Rightarrow {v_1}^2 = {u_1}^2 - 2{a_1}s$
Substitute $g + \dfrac{R}{M}$ for ${a_1}$ and $0\,{\text{m/s}}$ for ${v_1}$ in the above equation and rearrange it for the displacement $s$ of the ball.
${\left( {0\,{\text{m/s}}} \right)^2} = u_1^2 - 2\left( {g + \dfrac{R}{M}} \right)s$ …… (4)
$\Rightarrow s = \dfrac{{u_1^2}}{{2\left( {g + \dfrac{R}{M}} \right)}}$
Rewrite equation (3) for the displacement of the ball while going upward.
$\Rightarrow s = {u_1}{t_a} - \dfrac{1}{2}{a_1}t_a^2$
Here, ${t_a}$ is the time of ascent of the ball.
Substitute $g + \dfrac{R}{M}$ for ${a_1}$a in the above equation and rearrange it for ${t_a}$.
$\Rightarrow s = {u_1}{t_a} - \dfrac{1}{2}\left( {g + \dfrac{R}{M}} \right)t_a^2$
$\Rightarrow \dfrac{1}{2}\left( {g + \dfrac{R}{M}} \right)t_a^2 - {u_1}{t_a} + s = 0$
$\Rightarrow {t_a} = \dfrac{{{u_1} \pm \sqrt {u_1^2 - 2\left( {g + \dfrac{R}{M}} \right)s} }}{{g + \dfrac{R}{M}}}$
Substitute $0$ for $u_1^2 - 2\left( {g + \dfrac{R}{M}} \right)s$ in the above equation.
$\Rightarrow {t_a} = \dfrac{{{u_1} \pm \sqrt 0 }}{{g + \dfrac{R}{M}}}$ …… (from equation (4))
$\Rightarrow {t_a} = \dfrac{{{u_1}}}{{g + \dfrac{R}{M}}}$
Hence, the expression for time ascent the ball is $\dfrac{{{u_1}}}{{g + \dfrac{R}{M}}}$.
Calculate the time of descent of the ball while going downward.
Calculate the net acceleration ${a_2}$ on the ball when coming downward.

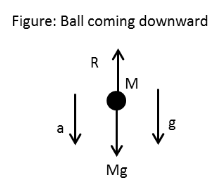
When the ball of mass $M$ is coming downward, the weight of the ball acts in downward direction and the air resistance acts in the upward direction.
Apply Newton’s second law to the ball.
$\Rightarrow R - Mg = - M{a_2}$
$\Rightarrow {a_2} = g - \dfrac{R}{M}$
Hence, net acceleration on the ball coming downward is $g - \dfrac{R}{M}$.
The final velocity of the ball when it reaches the ground is zero.
Let ${v_1}$ and ${v_2}$ are the initial and final velocities of the ball while coming downward and rewrite equation (3).
$\Rightarrow s = {v_1}{t_d} - \dfrac{1}{2}{a_2}t_d^2$
Here, ${t_d}$ is the time of descent of the ball.
Substitute $g - \dfrac{R}{M}$ for ${a_2}$ and $0\,{\text{m/s}}$ for ${v_1}$ in the above equation.
$\Rightarrow s = \left( {0\,{\text{m/s}}} \right){t_d} - \dfrac{1}{2}\left( {g - \dfrac{R}{M}} \right)t_d^2$
$\Rightarrow s = - \dfrac{1}{2}\left( {g - \dfrac{R}{M}} \right)t_d^2$
The displacement of the ball while moving upward and coming downward is the same.
Substitute $\dfrac{{u_1^2}}{{2\left( {g + \dfrac{R}{M}} \right)}}$ for $s$ in the above equation and solve for ${t_d}$.
$\Rightarrow \dfrac{{u_1^2}}{{2\left( {g + \dfrac{R}{M}} \right)}} = - \dfrac{1}{2}\left( {g - \dfrac{R}{M}} \right)t_d^2$
$\Rightarrow u_1^2 = \left( {g - \dfrac{R}{M}} \right)\left( {g + \dfrac{R}{M}} \right)t_d^2$
$\Rightarrow {t_d} = \dfrac{{u_1^2}}{{\left( {g - \dfrac{R}{M}} \right)\left( {g + \dfrac{R}{M}} \right)}}$
$\Rightarrow {t_d} = \sqrt {\dfrac{{u_1^2}}{{{g^2} - {{\left( {\dfrac{R}{M}} \right)}^2}}}}$ $\Rightarrow\because {a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)$
$\Rightarrow {t_d} = \dfrac{{{u_1}}}{{\sqrt {{g^2} - {{\left( {\dfrac{R}{M}} \right)}^2}} }}$
Hence, the expression for the time of descent of the ball is $\dfrac{{{u_1}}}{{\sqrt {{g^2} - {{\left( {\dfrac{R}{M}} \right)}^2}} }}$.

Note: The time of ascent for the ball moving upward and the time of descent for the ball coming downward are different when a constant air resistance is considered and same when air resistance is neglected.