Question

A ball of mass m hits the floor with a speed v making an angle $\theta =45{}^\circ$ of incidence with the normal to the floor. If the coefficient of restitution is $e=\dfrac{1}{\sqrt{2}}$ , find the speed of the reflected ball and angle of reflection.

Answer 1

In this question we have been asked to calculate the speed and angle of the ball after reflection. Therefore, we are basically to calculate the magnitude and direction of the velocity of the ball after hitting the floor. We have been given that the ball hits the floor at an angle of 45 degrees. The coefficient of restitution is also given. Therefore, using these two we shall first calculate the direction of velocity.

Complete step by step answer:
The ball makes an angle with the normal of the floor as shown in the figure below.

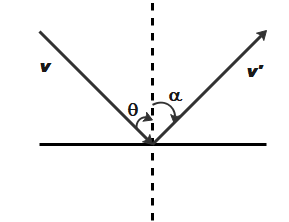
Therefore, the speed of ball in vertical direction will be given by,
${{V}_{y}}=v\cos \theta$
Similarly, the velocity along horizontal direction is given by,
${{V}_{x}}=v\sin \theta$
Now, it is given that coefficient of restitution is $e=\dfrac{1}{\sqrt{2}}$
Now, we know that after hitting the floor the velocity of ball will be given by,
${{V}_{y}}'=ev\cos \theta$ and the horizontal component of the velocity will remain same i.e. ${{V}_{x}}'=v\sin \theta$
Now, let us assume that the after hitting the ball makes an angle $\alpha$as shown in the figure.
We can say that,
$\tan \alpha =\dfrac{{{V}_{y}}'}{{{V}_{x}}'}$
After substituting the values
We get,
$\tan \alpha =\dfrac{ev\cos \theta }{v\sin \theta }$
On solving,
$\tan \alpha =e\cot \theta$
After substituting the given values
We get,
$\tan \alpha =\dfrac{1}{\sqrt{2}}\cot 45{}^\circ$
On solving,
$\tan \alpha =35.26{}^\circ$
Now we know that,
${{V}_{y}}'=ev\cos \theta$
Similarly,
${{V}_{x}}'=v\sin \theta$
After substituting values
We get,
${{V}_{y}}'=\dfrac{1}{\sqrt{2}}\times v\times \cos 35.26{}^\circ$, ${{V}_{x}}'=v\times \sin 35.26{}^\circ$
Therefore,
${{V}_{y}}'=0.577v$
Similarly,
${{V}_{x}}'=0.577v$
Now, we know that
$V'=\sqrt{{{V}_{x}}{{'}^{2}}+{{V}_{y}}{{'}^{2}}}$
Therefore,
$V'=\sqrt{{{0.577}^{2}}+{{0.577}^{2}}}$
On solving,
$V'=0.816v$
Therefore, the velocity of the ball after collision is 0.816v.

Note:
The coefficient of restitution is the ratio of the final velocity to initial relative velocity between the objects after they collide. The range of coefficient of restitution is from 0 to 1. If the value of coefficient of restitution is 1, the collision between the objects is said to be elastic. Therefore, it determines whether the collision is elastic or inelastic. The coefficient of restitution can not be greater than 1.