Solveeit Logo
Login

Question

Question: A ball of mass m hits the floor with a speed v making an angle of incidence \(\theta \) with the nor...

A ball of mass m hits the floor with a speed v making an angle of incidence θ\theta with the normal. The coefficient of restitution is e. The speed of reflected ball and the angle of reflection of the ball will be

(A) v′=v,θ=θ′v' = v,\theta = \theta '
(B) v′=v2,θ=2θ′v' = \dfrac{v}{2},\theta = 2\theta '
(C) v′=2v,θ=2θ′v' = 2v,\theta = 2\theta '
(D) v′=3v2,θ=2θ′3v' = \dfrac{{3v}}{2},\theta = \dfrac{{2\theta '}}{3}

Explanation

Solution

In order to solve above from first apply the law of conservation of momentum in x-direction and make an equation between v′,v,θv',v,\theta and θ′\theta '.
After then write formula of coefficient of restitution e
i.e., e == velocity of separation // velocity of approach
On putting the values vsep{v_{sep}} and vapp{v_{app}}, we will get an equation between v,v′,θv,v',\theta and θ′\theta '.
Now on solving these 2 equations, we will get desired solution.

Complete step by step answer:

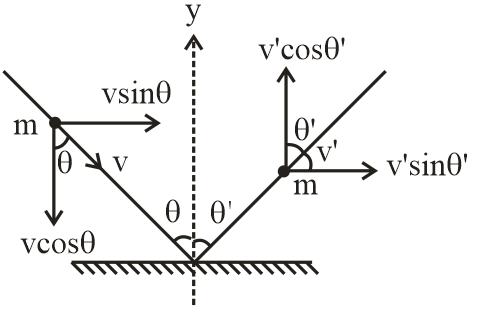
Given that a ball of mass m hits the floor i.e., collides with the floor and reflects back. So, we can use law of conservation of momentum i.e.,
Momentum before collision == Momentum after collision
We know that momentum is a vector quantity. So, we can use conservation law in both directions i.e., X and Y because the ball hits the ground at an angle θ\theta . Hence, from the diagram.
In x-direction
mvsin⁡θ=mv′sin⁡θ′mv\sin \theta = mv'\sin \theta '
vsin⁡θ=v′sin⁡θ′v\sin \theta = v'\sin \theta ' …..(1)
Here gravity acts on the ball that’s why we can not consider conservation of momentum is y-direction.
Here, coefficient of restitution is also given
i.e., e == velocity of separation // velocity of approach
Here
vsep=v′cos⁡θ′{v_{sep}} = v'\cos \theta '
vapp=vcos⁡θ{v_{app}} = v\cos \theta
So, e=v′cos⁡θ′vcos⁡θe = \dfrac{{v'\cos \theta '}}{{v\cos \theta }}
v′cos⁡θ′=evcos⁡θv'\cos \theta ' = ev\cos \theta …..(2)
Now, equation (1)2+(2)2{(1)^2} + {(2)^2}
(vsin⁡θ)2+(evcos⁡θ)2=(v′sin⁡θ′)2+(v′cos⁡θ′)2{(v\sin \theta )^2} + {(ev\cos \theta )^2} = {(v'\sin \theta ')^2} + {(v'\cos \theta ')^2}
  ⟹  v2sin⁡2θ+e2v2cos⁡2θ=v′2sin⁡2θ′+v′2cos⁡2θ′\implies {v^2}{\sin ^2}\theta + {e^2}{v^2}{\cos ^2}\theta = v{'^2}{\sin ^2}\theta ' + v{'^2}{\cos ^2}\theta '
  ⟹  v2(sin⁡2θ+e2cos⁡2θ)=v′2(sin⁡2θ′+cos⁡2θ′)\implies {v^2}({\sin ^2}\theta + {e^2}{\cos ^2}\theta ) = v{'^2}({\sin ^2}\theta ' + {\cos ^2}\theta ')
∵sin⁡2θ′+cos⁡2θ′=1\because {\sin ^2}\theta ' + {\cos ^2}\theta ' = 1
  ⟹  v′2=v2(sin⁡2θ+e2cos⁡2θ)\implies v{'^2} = {v^2}({\sin ^2}\theta + {e^2}{\cos ^2}\theta )
  ⟹  v′=v2(sin⁡2θ+e2cos⁡2θ)\implies v' = \sqrt {{v^2}({{\sin }^2}\theta + {e^2}{{\cos }^2}\theta )}
  ⟹  v′=vsin⁡2θ+e2cos⁡2θ\implies v' = v\sqrt {{{\sin }^2}\theta + {e^2}{{\cos }^2}\theta } …..(3)
For elastic collision e=1e = 1 …..(4)
So, v′=vsin⁡2θ+cos⁡2θv' = v\sqrt {{{\sin }^2}\theta + {{\cos }^2}\theta }
∴v′=v\therefore v' = v …..(5)
Now from equation 2, 4 and 5
v′cos⁡θ′=(1)v′cos⁡θv'\cos \theta ' = (1)v'\cos \theta
  ⟹  cos⁡θ′=cos⁡θ\implies \cos \theta ' = \cos \theta
⇒θ′=θ\Rightarrow \theta ' = \theta …..(6)
Hence from equation 5 and 6 we conclude that reflected angle and velocity is same as incident i.e.,
v′=v,θ′=θv' = v,\theta ' = \theta

So, the correct answer is “Option A”.

Note:
In many problems of collision, we can not get a final answer using only the law of momentum conservation. In that case we have to use the law of energy conservation also.
In elastic collision cases, we can also use the law of kinetic energy conservation also.