Solveeit Logo
Login

Question

Question: A ball of mass m hits a wall with a speed v making an angle\(\theta \) with the normal. If the coeff...

A ball of mass m hits a wall with a speed v making an angleθ\theta with the normal. If the coefficient of restitution is e, the direction and magnitude of the velocity of ball after reflection from the wall will respectively be:
A) tan⁡−1(tan⁡θe),(sin⁡2θ+cos⁡2θ)v{\tan ^{ - 1}}\left( {\dfrac{{\tan \theta }}{e}} \right),\left( {\sqrt {{{\sin }^2}\theta + {{\cos }^2}\theta } } \right)v
B) tan⁡−1(etan⁡θ),(1ve2sin⁡2θ+cos⁡2θ)v{\tan ^{ - 1}}\left( {\dfrac{e}{{\tan \theta }}} \right),\left( {\dfrac{1}{v}\sqrt {{e^2}{{\sin }^2}\theta + {{\cos }^2}\theta } } \right)v
C) tan⁡−1(etan⁡θ),vetan⁡θ{\tan ^{ - 1}}\left( {e\tan \theta } \right),\dfrac{v}{e}\tan \theta
D) tan⁡−1(etan⁡θ),vsin⁡θ+e2{\tan ^{ - 1}}\left( {e\tan \theta } \right),v\sqrt {\sin \theta + {e^2}}

Explanation

Solution

In order to find the solution we will follow the rule of angle of reflection which states that the angle of incidence is equal to angle of reflection and hence we will prove thatθ=θ′\theta = \theta '. The given condition is elastic in nature and hence the coefficient of restitution e will be equal to 1 which will eventually tell us the velocities before and after collision is the same.

Step by step solution:
Step 1:
We are given:
A ball of mass m hits a wall with a speed v making an angleθ\theta with the normal
The coefficient of restitution is e
Here we have a diagram to represent the various quantities.

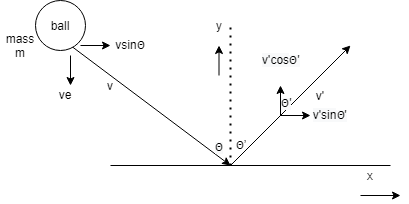
The ball is hitting the wall with the speed of v and reflected by the velocity v’. It makes an angle of θ\theta when hitting and then reflected by an angle ofθ′\theta '
The momentum will be conserved because no external force is being applied on the system before and after the hitting
This implies the momentum will be conserved in both x and y direction
The ball before and after hitting is moving along the x-direction and hence it is proceeding toward the sine component
The conservation of momentum for x will be mvsin⁡θmv\sin \theta =mg′sin⁡θ′mg'\sin \theta ' ……. (1)
From equation 1 we can say that vsin⁡θ=v′sin⁡θ′v\sin \theta = v'\sin \theta ' …… (2)
The coefficient of restitution e is defined as divide of velocity of separation divide by velocity of approach, e=vseparationvapproach\dfrac{{{v_{separation}}}}{{{v_{approach}}}} and from the diagram we can say that velocity of approach is vcos⁡θv\cos \theta and velocity of separation isv′cos⁡θ′v'\cos \theta '
So rewriting coefficient of restitution e=v′cos⁡θ′vcos⁡θ\dfrac{{v'\cos \theta '}}{{v\cos \theta }} ⇒v′cos⁡θ′=evcos⁡θ\Rightarrow v'\cos \theta ' = ev\cos \theta …….. (3)
Now squaring the equation 2 and 3 and adding them we get,(v′)2=v2(sin⁡2θ+e2cos⁡2θ){\left( {v'} \right)^2} = {v^2}({\sin ^2}\theta + {e^2}{\cos ^2}\theta )
Taking root both sides we get,v′=sin⁡2θ+e2cos⁡2θvv' = \sqrt {{{\sin }^2}\theta + {e^2}{{\cos }^2}\theta } v …… (4)
In elastic collision the coefficient of restitution e is equal to 1 and also the trigonometric identity sayssin⁡2θ+cos⁡2θ=1{\sin ^2}\theta + {\cos ^2}\theta = 1. Putting it in equation 4 we get, v′=vv' = v
Now dividing equation from equation 3, we get: tan⁡θ′=1etan⁡θ\tan \theta ' = \dfrac{1}{e}\tan \theta ….. (5)
As we have said that it is elastic collision so coefficient of restitution will be 1 thenθ′=θ\theta ' = \theta
Angle of incidence is equal to angle of reflection.

Hence, from equation 4 and 5 our correct option is A.

Note: There is a rule of separating two vectors from the component. When we separate them then the side which is closer to the angle made by them will be called as cos⁡θ\cos \theta and the angle made by it far from the component will be called as sin⁡θ\sin \theta as shown in the figure above. They are perpendicular to each other.