Question

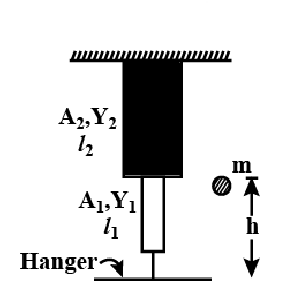
A ball of mass ‘$m$’ drops from a height ‘$h$’ which sticks to mass less hanger after striking. Neglect overturning, find out the maximum extension in the rod. Assuming the rod is massless.

Answer 1

When attempting questions like the one given to us above, keep in mind the concepts regarding Young’s modulus and the conservation of energy theorem and know when and where to apply them in the question for easier and fast calculation.

Complete step-by-step answer:

Young’s modulus is one property of solids which tells us how easily a material stretches and deforms. Materials which obey the Hooke’s law , use the formula of $F=kx$where $F$is the force applied, which will extend the material to a distance of $x$and $k$is the spring constant.
For easier understanding, Young’s modulus ($E$) is a property of the material that tells us how easily it can stretch and deform and is defined as the ratio of tensile strength ($\sigma$) to tensile strain ($\varepsilon$) . Where stress is the amount of force applied per unit area ($\sigma =\dfrac{F}{A}$) and strain is extension per unit length ($\varepsilon =\dfrac{dl}{l}$)
$E=\dfrac{\sigma }{\varepsilon }=\dfrac{\dfrac{F}{A}}{\dfrac{dl}{l}}$
Where $E$or $Y$ is the Young’s modulus
$\sigma$is the tensile strength or $\sigma =\dfrac{F}{A}$
$\varepsilon$ is the tensile strain or $\varepsilon =\dfrac{dl}{l}$
Now one may ask , Does Young’s modulus change with length? The answer to that is no , Young’s modulus does not change with length. The reason is that if the length or diameter is increased the value of stress increases and consequently there will be an increase in expansion and the strain .
Although keep in mind that Young’s modulus is meaningful only in the range in which the stress is proportional to the strain , and the material returns to its original dimensions when the external force is removed. As stresses increase , the material may either flow, undergoing permanent deformation, or finally break.
For easier calculation, assume the maximum extension in rod to be ${{x}_{\max }}$ ,
Applying the energy conservation theorem ,
$mg(h + x) = \dfrac{1}{2}\dfrac{{{k_1}{k_2}}}{{{k_1} + {k_2}}}{x^2}$
Where ${k_1} = \dfrac{{{A_1}{Y_1}}}{{{l_1}}}$
And ${k_2} = \dfrac{{{A_2}{Y_2}}}{{{l_2}}}$
And ${k_{eq}} = \dfrac{{{A_1}{A_2}{Y_1}{Y_2}}}{{{A_1}{Y_1}{l_1} + {A_2}{Y_2}{l_2}}}$
${k_{eq}}{x^2} - 2mgx - 2mgh = 0$
$x = \dfrac{{2mg \pm \sqrt {4{m^2}{g^2} + 8mgh{k_{eq}}} }}{{2{k_{eq}}}}$
$\therefore {x_{\max }} = \dfrac{{mg}}{{{k_{eq}}}} + \sqrt {\dfrac{{{m^2}{g^2}}}{{k_{eq}^2}} + \dfrac{{2mgh}}{{{k_{eq}}}}}$

Note: The Young's modulus often depends on the orientation of a material. Isotropic materials display mechanical properties that are the same in all directions. Working a material or adding impurities to it can produce grain structures that make mechanical properties directional. These anisotropic materials may have very different Young's modulus values, depending on whether force is loaded along the grain or perpendicular to it. Good examples of anisotropic materials include wood, reinforced concrete, and carbon fiber.