Question

A ball of mass $m = 200gm$ is suspended from a point A by an inextensible string of length $L$ . Ball is drawn to a side and held at the same level as A but at a distance $\dfrac{{\sqrt 3 }}{2}L$ from A as shown. Now the ball is released. Then: (assume string applies only that much jerk which is required so that velocity along string becomes zero).

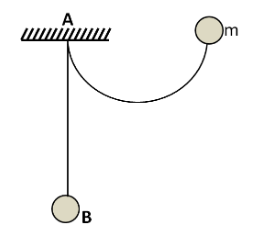
(A) Speed of ball just before experiencing jerk is $\sqrt {gL}$
(B) Speed of ball just after experiencing jerk is $\dfrac{{\sqrt {3gL} }}{2}$
(C) Impulse applied by string is $\dfrac{{\sqrt {gL} }}{{10}}$
(D) Ball will experience jerk after reaching point B.

Answer 1

Hint : The ball when it will experience the jerk, when the string will become taut, whose position can be determined easily. Then, using the theorem of conservation, we can find out the speed of the ball just before experiencing the jerk. Finally, breaking the components of the velocity in directions along and perpendicular to the string, we will get both the speed after jerk, and the impulse.

Formula used: The formula used to solve this question is given by
$I = \Delta p$ , $I$ is the impulse, and $\Delta p$ is the change in momentum.

Complete step by step answer
We know that a string can apply the force of tension only when it is taut. So the string will not apply any jerk on the ball until it is taut. Once it becomes taut, it will apply the jerk on the ball along the direction of the string. Let us consider a point P at which the string becomes taut, so that $AP = L$ , as shown below.

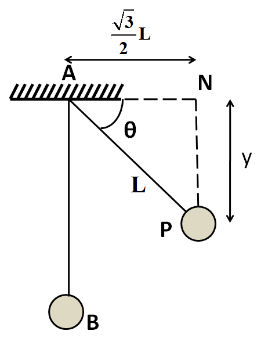
From the above figure we have
$\sin {{\theta }} = \dfrac{y}{{AP}}$
$\sin {{\theta }} = \dfrac{{L/2}}{L} = \dfrac{1}{2}$
Taking sine inverse both the sides, we get
${{\theta }} = {30^ \circ }$ -------(1)
Applying Pythagoras theorem in the triangle ANP, we have
$A{P^2} = P{N^2} + A{N^2}$
$\Rightarrow {L^2} = {y^2} + A{N^2}$
Since the horizontal distance of the ball from point A is equal to $\dfrac{{\sqrt 3 }}{2}L$ , so we have $AN = \dfrac{{\sqrt 3 }}{2}L$ . Therefore we have
${L^2} = {y^2} + {\left( {\dfrac{{\sqrt 3 }}{2}L} \right)^2}$
$\Rightarrow {L^2} = {y^2} + \dfrac{{3{L^2}}}{4}$
Subtracting $\dfrac{{3{L^2}}}{4}$ from both the sides, we have
${y^2} = {L^2} - \dfrac{{3{L^2}}}{4}$
$\Rightarrow {y^2} = \dfrac{{{L^2}}}{4}$
Taking square root both sides, we get
$y = \dfrac{L}{2}$ -------(2)
So after falling a vertical distance of $\dfrac{L}{2}$ the string is becoming taut and hence the ball will experience jerk before reaching the point B.
Hence, the option D is incorrect.
Now, let $v$ be the speed of the ball just before experiencing the jerk.
Since it falls under the conservative gravitational force, it’s mechanical energy remains conserved. Therefore, the potential energy at A will be equal to the kinetic energy at B.
$\dfrac{1}{2}m{v^2} = mgy$
$\Rightarrow {v^2} = 2gy$
From equation (2)
${v^2} = 2g\left( {\dfrac{L}{2}} \right)$
$\Rightarrow {v^2} = gL$
Taking square root both sides, we get
$v = \sqrt {gL}$ -------(3)
Thus, the speed of ball just before experiencing jerk is equal to $\sqrt {gL}$
Hence, the option A is correct.
Now, as the ball is falling vertically, so this velocity will be in the vertically downwards direction. Breaking its components along the string, and perpendicular to it, we get

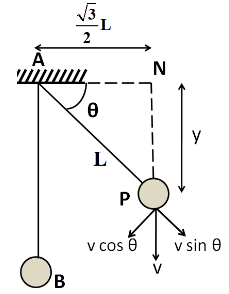
According to the question, the jerk of the string is just sufficient to make the velocity along the string equal to zero. So the component $v\sin {{\theta }}$ becomes zero after the jerk. We know that the impulse is given by
$I = \Delta p$
$\Rightarrow I = mv\sin {{\theta }} - m\left( 0 \right)$
From equation (1)
$I = mv\sin {30^ \circ } = \dfrac{{mv}}{2}$
From (3)
$I = \dfrac{{m\sqrt {gL} }}{2}$
According to the question, $m = 200g = 0.2kg$ . Substituting this above, we get
$I = \dfrac{{0.2\sqrt {gL} }}{2}$
$\Rightarrow I = \dfrac{{\sqrt {gL} }}{{10}}$
Thus, the impulse applied by string is equal to $\dfrac{{\sqrt {gL} }}{{10}}$
Hence, the option C is also correct.
As the component of velocity along the string becomes zero, so the ball will have only the velocity along the line perpendicular to the string after the jerk, which is given by
$v' = v\cos {{\theta }}$
From equation (1) and (3)
$v' = \sqrt {gL} \cos \left( {{{30}^ \circ }} \right)$
$v' = \dfrac{{\sqrt {3gL} }}{2}$
Therefore the speed of the ball after experiencing the jerk is equal to $\dfrac{{\sqrt {3gL} }}{2}$ .
Hence, the option B is also correct.
Therefore the correct answers are A, B, and C.

Note
We should not forget to convert the CGS unit, gram of the mass of the ball given into the SI unit, kilogram. Also, the force of tension will take an infinitely small amount of time to make the velocity of the ball along the string equal to zero. During this time, the force of tension will be very large.