Question

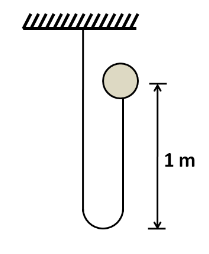
A ball of mass $1kg$ is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut. (Take $g = 10m/{s^2}$ )

Answer 1

Hint : We need to use the energy conservation principle to find out the velocity of the ball just before the string becomes taut. Then, finding the change in momentum of the ball, at the bottom point, we will get the required value of impulse.

Formula used: The formula used to solve this question is given by
$p = mv$ , $p$ is the momentum of a particle of mass $m$ which is moving with a velocity of $v$ .

Complete step by step answer
As the ball is released vertically, it will fall in the vertically downward direction. We know that a string can apply the force of tension only when it is taut. As during the whole vertical motion of the ball, the string is loose, so the force of tension will remain zero during this interval. So the ball will only be acted upon by the gravitational force of the earth. Therefore, its mechanical energy will be conserved, from the time of release to the instant just before the string becomes taut.
Let the velocity of the ball at the bottommost point be $v$ . As the ball falls downwards, its potential energy will be converted into the kinetic energy. So the kinetic energy of the ball at the bottom will be equal to its potential energy at the top, that is,
$\dfrac{1}{2}m{v^2} = mg\left( {2h} \right)$ (ball will fall twice the height to reach downwards)
$\Rightarrow {v^2} = 4gh$
Taking square root both the sides, we get
$v = 2\sqrt {gh}$ --------(1)
Now, when the ball reaches the bottom, the string will become taut and therefore will apply a force of tension on the ball, which will be vertically upwards. Since the velocity of the ball is vertically downwards, the force of tension will make the velocity of the ball zero.
We know that the impulse is equal to the change in momentum. So the impulse imparted by the string to the ball immediately after the string becomes taut is
$I = {p_f} - {p_i}$
$I = m\left( 0 \right) - mv$
From equation (1)
$I = - 2m\sqrt {gh}$
According to the question, $m = 1kg$ , and $h = 1m$ . Putting these above we get
$I = - 2\sqrt g$
Substituting $g = 10m/{s^2}$
$I = - 2\sqrt {10} = - 6.32kgm/s$
Taking the magnitude, we get the impulse equal to $6.32kgm/s$ .

Note
The force of tension will act for an infinitely small amount of time to make the ball at rest. Thus the ball will come to rest almost instantly. During this time, the force of tension will be very large.