Question
Question: A ball of mass \(1kg\) is at rest in position P by means of two light strings OP and RP. The string ...
A ball of mass 1kg is at rest in position P by means of two light strings OP and RP. The string RP is now cut and the ball swings to position Q. Find the tensions in the string in position OP (when RP was not cut) and OQ (when RP was cut ). (Take g=10m/s2).
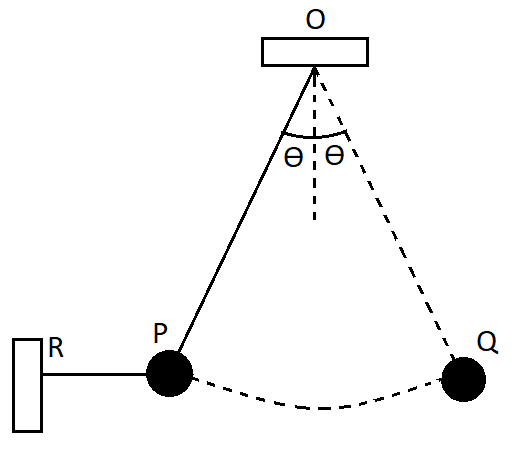
Solution
Hint
We need to draw the free body diagram in both the cases on the ball. Then as in both the cases the ball is at rest, the total force on the ball will be zero. So equating the forces in the two cases, we get the tension in the string.
In this solution, we will be using the following formula,
⇒Fnet=ma
Where Fnet is the net force acting on the body of mass m, causing an acceleration a.
Complete step by step answer
To find the tension in the first case, we first need to draw the free body diagram for the first case. In this case, the ball is at rest. So the total forces acting on the ball will cancel out each other. Now the forces are the force of tension along the string OP and the mass of the ball in the downward direction. So we can draw the figure as,
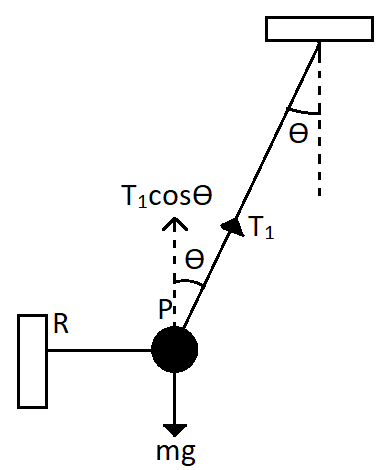
Here we have taken the tension in the string as T1. So the cosine component of the tension T1 will be balancing the weight of the ball in order for the net force on the ball to be zero.
So we can write the equation of motion of the ball as,
⇒T1cosθ−mg=0
We can take the mg to the RHS of the equation and have
⇒T1cosθ=mg
To find the tension T1 we take the cosθ to the other side.
So we get,
⇒T1=cosθmg
Now by substituting the values, m=1kg, g=10m/s2 and the angle θ=45∘. Then we get
⇒T1=cos45∘1×10
The value of cos45∘ is 21
So substituting,
⇒T1=2110
Hence, on calculating, we have the tension in the first case as,
⇒T1=102N
For the second case when the string is cut and the ball reaches the position Q, the ball will again come to rest momentarily. So the net force acting on the body will be zero. Therefore, we can draw the free body diagram using the tension and the mass of the ball as,
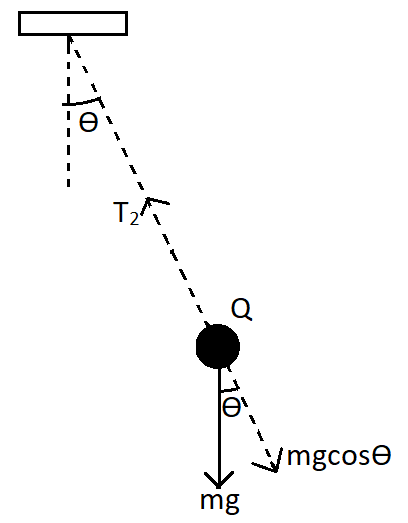
Here we have the tension as T2 and mass of the body mg acting downwards. Since the total force is zero, the cosine component of the mass will be balancing the tension.
⇒T2−mgcosθ=0
Therefore, we can write by taking mgcosθ to the RHS we get
⇒T2=mgcosθ
By substituting m=1kg, g=10m/s2 and θ=45∘, then we get the value of the tension as,
⇒T2=1×10cos45∘
The value of cos45∘ is 21
So substituting we get
⇒T2=21×10
Therefore, on multiplying 2 in numerator and denominator we get,
⇒T2=2102
On cancelling 2 we get
⇒T2=52N
So this is the tension in the string in the second case.
Note
Free body diagrams in physics are used to visualize the applied forces and the resulting actions on a body due to those forces. They consist of a simple version of the body and the forces drawn with straight line arrows. And the momentums are drawn with curved lines if necessary to depict the direction of motion of the body.
