Solveeit Logo
Login

Question

Question: A ball of mass 0.4 kg hits a brick wall. The ball strikes when it is moving horizontally to the left...

A ball of mass 0.4 kg hits a brick wall. The ball strikes when it is moving horizontally to the left at 30ms−130m{{s}^{-1}} and rebounds horizontal at 20ms−120m{{s}^{-1}}. Find the impulse of the force exerted on the ball by the wall.
A. 20Ns\text{A}\text{. 20Ns}
B. 4Ns\text{B}\text{. 4Ns}
C. 14 Ns\text{C}\text{. 14 Ns}
D. 8Ns\text{D}\text{. 8Ns}

Explanation

Solution

When a large force acts on a body for short time duration, the change it produces in its momentum is known as impulse. In our daily life, we come across many problems where force and time are difficult to ascertain separately. The impulse, in such cases, becomes an important measurable quantity.
Impulse can be calculated by determining change in momentum of the ball after rebounding from the wall.
Formula Used:
Impulse I⃗=mΔv⃗\vec{I}=m\Delta \vec{v}

Complete answer:
Impulse is the change in momentum produced, when a large force acts on a body for a short period of time. In such cases, it is difficult to determine force and time duration separately. That is where impulse comes into play as change in momentum can be calculated. Mathematically, we can write impulse
I⃗=mΔv⃗\vec{I}=m\Delta \vec{v}
Where m is the mass of the body and Δv⃗\Delta \vec{v} is the change in the velocity vector.
We are given that mass of the ball is 0.4 kg, its initial velocity, 30ms−130m{{s}^{-1}} and final velocity, 20ms−120m{{s}^{-1}} in direction opposite to initial velocity.

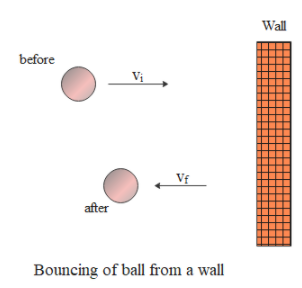
Therefore change in velocity of the ball
Δv⃗=v⃗f−v⃗i\Delta \vec{v}={{\vec{v}}_{f}}-{{\vec{v}}_{i}}
Assuming direction of initial velocity as positive, we get
Δv⃗=(−20ms−1)−30ms−1=−50ms−1\Delta \vec{v}=(-20m{{s}^{-1}})-30m{{s}^{-1}}=-50m{{s}^{-1}}
We substitute this result and get
I⃗=(0.4kg)×(−50ms−1)\vec{I}=(0.4kg)\times (-50m{{s}^{-1}})
I⃗=−20 kg ms−1=−20Ns\vec{I}=-20\text{ }kg\text{ }m{{s}^{-1}}=-20Ns
Thus the impulse of the force exerted by brick wall on the ball is
⇒∣I⃗∣=20Ns\Rightarrow \left| {\vec{I}} \right|=20Ns

Hence, option A is correct.

Note:
Velocity is a vector quantity and when it bounces back from the wall its direction changes. Thus, when we calculate change in velocity vector, direction must be considered.
Since, momentum is a vector quantity, impulse is also a vector.