Question

A ball of density $\rho$ is gently released in a liquid of density $\delta$, where $\rho>\delta$. What will be the acceleration of free fall of the ball in the liquid?
A.g
B.$(\rho - \delta)g$
C.$\dfrac{(\rho - \delta)g}{\rho}$
D.$\dfrac{\rho g}{(\rho - g)}$

Answer 1

Recall that the motion of the ball through the liquid produces a displacement of the volume of the liquid. This is brought about by contributions from the buoyant force that acts upwards against the motion of the ball. The other contributing force is the gravitational force that acts downwards. So, use a free body diagram to determine the net force acting on the ball, which in turn facilitates the acceleration of the ball through the liquid, for which you can then establish a relation.
Formula Used:
Buoyant force exerted by a liquid at rest $F_{B} = m_{liquid}g = V\delta g$
Gravitational force $F_{G} = mg = \rho V$

Complete answer:
We have a liquid of density $\delta$, and a ball of density $\rho$ that is gently released into the liquid. Let the volume of the ball be $V$. Then, the volume of water displaced by the liquid as a consequence of the motion of this ball through it is also $V$.
Therefore, the buoyant force $F_{B}$ exerted by the liquid on the ball is given as:
$F_{B} = m_{liquid}g = V\delta g$, since mass is volume times density.
The weight of the ball can be given as the gravitational force acting on it:
$F_{G} = m_{ball}g = V\rho g$

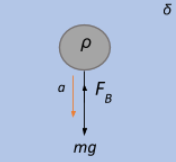
Since the density of the ball is greater than that of the liquid, the ball does not float in the liquid but falls through the liquid. It undergoes an acceleration as a consequence of this fall. Therefore, the net acceleration of the ball will be contributed by the difference between the gravitational and the buoyant forces acting on the ball, i.e.,
$F_{net} = F_{G} – F_{B}$
$\Rightarrow m_{ball}a = m_{ball}g – m_{liquid}g$
$\Rightarrow V\rho a = V\rho g – V\delta g$
$\Rightarrow \rho a = (\rho-\delta)g \Rightarrow a = \dfrac{(\rho-\delta)g}{\rho}$

Therefore, the correct choice would be C. $\dfrac{(\rho-\delta)g}{\rho}$

Note:
Always use free body diagrams to summarize the list of all influencing forces in a system as this ensures that all forces are accounted for.
On a specific note, do not forget that the magnitude of buoyant force can be derived by calculating the volume of the liquid displaced by a body immersed in it, though buoyancy is a characteristic of the liquid (and not the immersed body), and is directly proportional to the density of the liquid.