Question

A ball moving with speed $20\,m{s^{ - 1}}$ collides with a smooth surface as shown in the figure. The magnitude of change in velocity of the ball will be

A. $10\sqrt 3 \,m{s^{ - 1}}$
B. $20\sqrt 3\,m{s^{ - 1}}$
C. $\dfrac{{40}}{{\sqrt 3 }}\,m{s^{ - 1}}$
D. $40\,m{s^{ - 1}}$

Answer 1

In order to solve this question, we will calculate the velocities in vector form in two dimensional Cartesian XY plane and then resolve its components in each direction in both initial and final velocities then will find the change in velocity hence using magnitude formula, we will find the magnitude of change in velocity.

Complete step by step answer:
Let us first draw the components of initial and final velocities in free body diagram, we can see from the geometry of diagram such that,

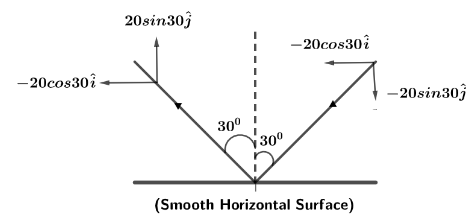
Initial velocity in vector form can be written as
${v_{initial}} = ( - 20\sin {30^0}\hat i - 20\cos {30^0}\hat j)$
Since, X component and the Y component both are in negative direction.
Now, the final velocity from the diagram can be written in vector form as
${v_{final}} = ( - 20\sin {30^0}\hat i + 20\cos {30^0}\hat j)$

Now, as we need to find the change in velocity which can be written as
Change in velocity $\Delta v = {v_{final}} - {v_{initial}}$ or
$\Delta v = ( - 20\sin {30^0}\hat i + 20\cos {30^0}\hat j) - ( - 20\sin {30^0}\hat i - 20\cos {30^0}\hat j)$
$\Rightarrow \Delta v = 40\cos {30^0}\hat j$
Put the value of $\cos {30^0} = \dfrac{{\sqrt 3 }}{2}$ we get
$\Delta v = 40 \times \dfrac{{\sqrt 3 }}{2}\hat j$
$\Rightarrow \Delta v = 20\sqrt 3 \hat j$
Now, the magnitude of change in velocity can be written as
$\left| {\Delta v} \right| = 20\sqrt 3$
So, the change in velocity of the ball is $\left| {\Delta v} \right| = 20\sqrt 3$.

Hence, the correct option is B.

Note: It should be remembered that, the velocity component in Y direction only changes while ball continues to move with same velocity in X direction, and if a vector is written in the form of $\vec v = a\hat i + b\hat j + c\hat k$ , then the magnitude of this vector is calculated by the formulas as $\left| {\vec v} \right| = \sqrt {{a^2} + {b^2} + {c^2}}$.