Question

A ball is thrown vertically upwards from the ground. It crosses a point at the height of 25m twice at an interval of 4 s. The ball was thrown with the velocity of –
A) 20 $m{{s}^{-1}}$
B) 25 $m{{s}^{-1}}$
C) 30 $m{{s}^{-1}}$
D) 35 $m{{s}^{-1}}$

Answer 1

We need to understand the relation of the initial velocity and the height attained with respect to the time and the total time taken to get the required initial velocity. The equations of motion have to be used correctly in order to solve.

Complete answer:
We are given a motion of a body against the gravitational force in one dimension. The body is projected vertically upwards with an initial velocity such that it moves against the acceleration due to gravity and reaches a maximum height. We know that on reaching the maximum height the velocity becomes zero and the body starts to travel downwards.

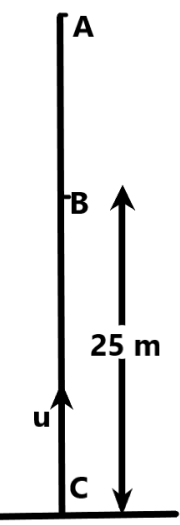
We are given that the object moves above 25 m height and the returns to this point after 4 seconds. Let us consider the 25m point above the ground as a reference point which has an initial velocity and the time period as 4 seconds. We can find the velocity 25 m above the ground using the equations of motion as –

& {{T}_{B}}=\dfrac{2{{u}_{B}}}{g} \\\ & \Rightarrow {{T}_{B}}=4s=\dfrac{2{{u}_{B}}}{10m{{s}^{-2}}} \\\ & \therefore {{u}_{B}}=20m{{s}^{-1}} \\\ \end{aligned}$$ So, know we can find the height travelled from the point B as – $$\begin{aligned} & {{h}_{AB}}=\dfrac{{{u}_{B}}^{2}}{2g} \\\ & \Rightarrow {{h}_{AB}}=\dfrac{{{20}^{2}}}{2(10)} \\\ & \therefore {{h}_{AB}}=20m \\\ \end{aligned}$$ So, the total height travelled by the body is – $$\begin{aligned} & h={{h}_{AB}}+{{h}_{BC}} \\\ & \Rightarrow h=20m+25m \\\ & \therefore h=45m \\\ \end{aligned}$$ Now, we can find the initial velocity of the body from the ground using the height attained by the body as – $$\begin{aligned} & h=\dfrac{{{u}^{2}}}{2g} \\\ & \Rightarrow 45m=\dfrac{{{u}^{2}}}{2(10)} \\\ & \Rightarrow u=\sqrt{900} \\\ & \therefore u=30m{{s}^{-1}} \\\ \end{aligned}$$ The initial velocity of the body is $$30m{{s}^{-1}}$$. **The correct answer is option C.** **Note:** The vertical upward projectile of a body is a special case of a projectile motion. In the vertical case, the projectile will be in right angles to the horizontal and all the cosine components will be zero and as such is the range of the projectile also.