Question

A ball is thrown vertically upward; it has a speed of 10m/s when it has reached one half of its maximum height. How high does the ball rise? (Taking $g = 10m/{s^2}$)

Answer 1

Hint – To solve such types of questions we need to solve using equations of motion. We will put the final velocity zero and calculate the height by putting the value of height half of the maximum height using the variable h and use the information provided in the problem to get the right answer.

Formula used: ${v^2} - {u^2} = 2as$

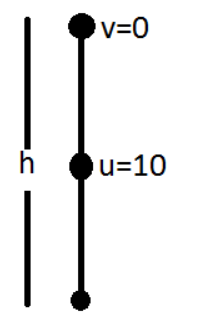
Complete step-by-step answer:
Given, initial speed of ball=10m/s
Let the maximum height be h.
We know that, ${v^2} - {u^2} = 2as$
Putting the value of v= 0, u = 10, a = g = 10, ${\text{s = }}\dfrac{{\text{h}}}{{\text{2}}}$.
$0 = {u^2} - 2g(h/2) \\\ h = \dfrac{{{u^2}}}{g} = \dfrac{{{{(10)}^2}}}{{10}} = 10m \\\$
Hence, the answer to this question is 10m.

Note – In such types of questions, we should consider the upper ward direction as positive and downward direction negative. Displacement in the nth second, $S = u + \dfrac{a}{2}(2n - 1)$. We need to use equations of motion when the acceleration is constant. Since, acceleration due to gravity is constant on earth so we have used equations of motion. Equations of motion are: $v = u + at,\,\,S = ut + \dfrac{1}{2}a{t^2},\,\,{v^2} - {u^2} = 2as$.
We suggest students to know the derivation of these equations. It will clear your concept more deeply and knowing these equations will help you further.