Question
Question: A ball is thrown vertically up (taken \[as{\text{ }} + z\] axis) from the ground. The correct moment...
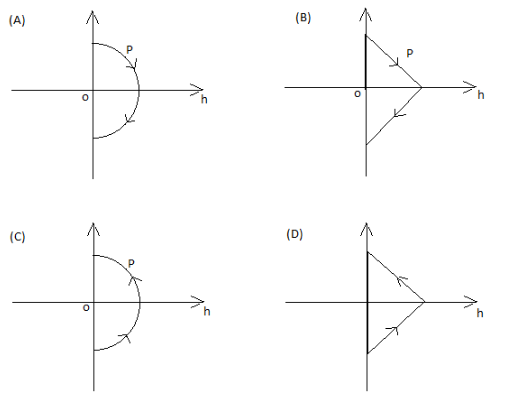
A ball is thrown vertically up (taken as +z axis) from the ground. The correct momentum height (p−h) diagram is :
Solution
Momentum, product of the mass of a particle and its velocity.
Momentum is a vector quantity as it has both magnitude and direction. It can be used to predict the resulting direction and speed of motion of objects after they collide. We can use the equation of motions under gravity,
Height h=2gu2−p2/m2
Complete step by step answer:
We know that equation for Momentum p = mv$$$$.......\left( 1 \right)
m is the mass of the body.
v is the velocity of the body.
For the motion under gravity
Height h = \dfrac{{{u^2} - {p^2}/{m^2}}}{{2g}}$$$$ \ldots ..\left( 2 \right)
u is the initial velocity of the mass.
g is the acceleration due to gravity.
g=9.8m/s2
h=2gu2−p2/m2
h=2gu2−2gmp2
This is exactly like a parabolic relation so we have two options that seem to be the same graph, but the direction of momentum shown is opposite. So for finding the direction of momentum we can further investigate the problem with the direction of velocity. We can consider the upward motion, velocity is positive, mass is a constant here. So the momentum is also positive. We can consider the downward motion, velocity is opposite direction. So it is negative. This also tells us the momentum is also negative. From our last equation, we can conclude that the velocity and height have a parabolic relationship.
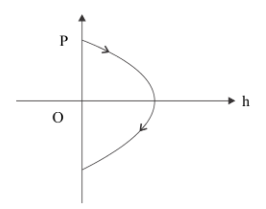
So the connect answer is option (A).
Note: There are two kinds of momentum linear and angular. A spinning object has angular momentum; an object traveling with a velocity has linear momentum. The most common symbol for momentum is P. The SI unit for momentum is kg m/s. The dimensional formula for the momentum is MLT−1. Momentum is conserved always in any type of collision.
