Question

A ball is thrown vertically downwards from a height of $20m$ with an initial velocity ${v_ \circ }$. It collides with the ground and loses $50\%$ of its energy in the collision and rebounds to the same height. The initial velocity ${v_ \circ }$ is:
A) $14m{s^{ - 1}}$
B) $20m{s^{ - 1}}$
C) $28m{s^{ - 1}}$
D) $10m{s^{ - 1}}$

Answer 1

This motion is not a free fall and has some initial velocity to it. The ball initially has some kinetic energy and potential energy. As the ball moves downwards the potential energy decreases and the kinetic energy increases. Use the law of conservation of energy before and after the collision.

Complete step by step solution:
The ball is thrown vertically downwards with some initial velocity. Thus we know that is not a freefall motion. The ball will have some initial kinetic energy along with the potential energy.

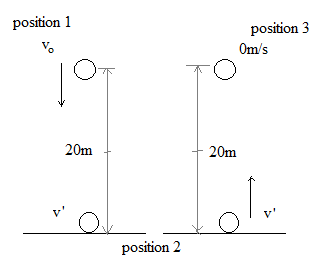
The above diagram depicts the given condition.
Now we all know that energy can neither be created nor be destroyed. It can only change its form. The energy will always be conserved.
Here in this case let us see what is happening. The ball has some initial velocity and is initially at a certain height from the ground. Thus there is some potential energy stored in the ball initially and the ball has some initial kinetic energy as well. Now when the ball is moving downwards, its distance from the ground is decreasing and so is the potential energy. The decrease in the height results in the loss of potential energy.
Then on collision as per the question $50\%$ of the energy is lost. So now the ball has only kinetic energy and because of that the ball moves in the upward direction again moreover rebounds to the same height. Now the height of the ball is increasing and so the ball starts gaining some potential energy. Finally the ball reaches the initial height and there the kinetic energy is lost completely and the final velocity of the ball will be zero.
So, if initial velocity is ${v_ \circ }$, $H$ is the height from the ground and $v'$ is the velocity at ground we can write for the motion before collision
${E_1} = PE + KE$
$\Rightarrow {E_1} = mgH + \dfrac{1}{2}m{v_ \circ }^2$
Here, ${E_1}$ is the total energy before collision at position 1.
Now for energy at position 2 we have;
$\Rightarrow {E_2} = \dfrac{1}{2}m{(v')^2}$
And for position 3 we have;
$\Rightarrow {E_3} = mgH$
Now according to the question we have
$\Rightarrow {E_3} = \dfrac{1}{2}{E_1}$
So, substituting the values we get;
$\Rightarrow mgH = \dfrac{1}{2}mgH + \dfrac{1}{4}m{v_ \circ }^2$
Solving the above equation we get;
$\Rightarrow \dfrac{1}{4}m{v_ \circ }^2 = \dfrac{1}{2}mgH \\\ \Rightarrow {v_ \circ } = \sqrt {2gH} \\\ \Rightarrow {v_ \circ } = \sqrt {2 \times 10 \times 20} \\\ \therefore {v_ \circ } = 20m{s^{ - 1}}$

Therefore, option B is correct.

Note: Before collision and after collision the momentum remains conserved. The energy is also conserved. Energy can neither be created nor be destroyed but can only be transformed from one part to another. If the ball was undergoing a free fall motion then the initial velocity would have been zero. Then the ball would not have the initial kinetic energy.