Question

A ball is thrown upwards from the ground with an initial speed of u. At two instants of time, having an interval of 6 s, the ball is at a height of 80 m from the ground. Find u. Take g = 10 $\text{ms}^{-2}$.

Answer 1

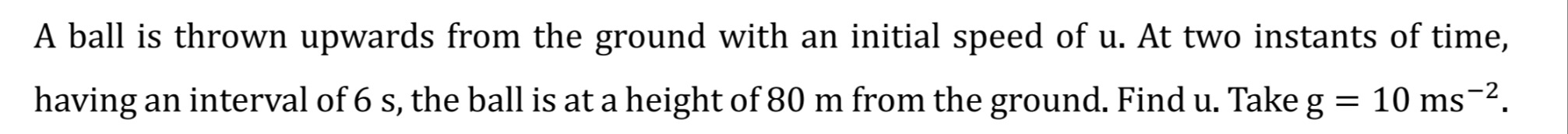
50

Answer 2

The motion of the ball is governed by the equation of kinematics for vertical motion under gravity:

$h = ut - \frac{1}{2}gt^2$

Given:

Height, $h = 80$ m Acceleration due to gravity, $g = 10 \text{ ms}^{-2}$ Time interval, $\Delta t = t_2 - t_1 = 6$ s

Substitute the given values into the equation:

$80 = ut - \frac{1}{2}(10)t^2$ $80 = ut - 5t^2$

Rearrange this into a standard quadratic equation in terms of time $t$:

$5t^2 - ut + 80 = 0$

Let $t_1$ and $t_2$ be the two instants of time when the ball is at a height of 80 m. These are the roots of the quadratic equation.

From the properties of quadratic equations $ax^2 + bx + c = 0$:

Sum of roots: $t_1 + t_2 = -\frac{(-u)}{5} = \frac{u}{5}$ Product of roots: $t_1 t_2 = \frac{80}{5} = 16$

We are given the difference between the two times:

$t_2 - t_1 = 6$

Now we have a system of equations:

1. $t_1 + t_2 = \frac{u}{5}$
2. $t_1 t_2 = 16$
3. $t_2 - t_1 = 6$

From equation (3), express $t_2$ in terms of $t_1$:

$t_2 = t_1 + 6$

Substitute this into equation (2):

$t_1(t_1 + 6) = 16$ $t_1^2 + 6t_1 - 16 = 0$

Solve this quadratic equation for $t_1$. We can factor it:

$(t_1 + 8)(t_1 - 2) = 0$

This gives two possible values for $t_1$: $t_1 = -8$ s or $t_1 = 2$ s. Since time cannot be negative in this physical context (it's the first time the ball reaches 80m after launch), we take $t_1 = 2$ s.

Now, find $t_2$ using $t_2 = t_1 + 6$:

$t_2 = 2 + 6 = 8$ s

Finally, substitute the values of $t_1$ and $t_2$ into equation (1) to find $u$:

$t_1 + t_2 = \frac{u}{5}$ $2 + 8 = \frac{u}{5}$ $10 = \frac{u}{5}$ $u = 10 \times 5$ $u = 50 \text{ ms}^{-1}$

The initial speed of the ball is 50 m/s.