Question
Question: A ball is thrown upwards from earth’s surface with a speed \(3{{v}_{e}}\), when the ball crosses ear...
A ball is thrown upwards from earth’s surface with a speed 3ve, when the ball crosses earth’s gravitational field, then, (ve is escape velocity)
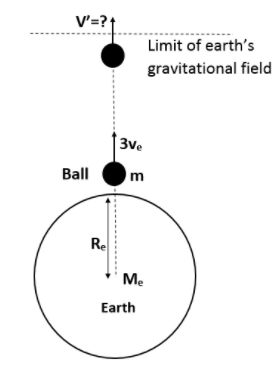
A)v′=2veB)v′=7veC)v′=22veD)v′=ve
Solution
To solve this question, we will use the law of conservation of energy. We will calculate the total energy of the ball at earth surface which will be the sum of both kinetic and potential energy. This energy will be equal to the total energy at the limit of earth’s gravitational field. We must know that, at above earth’s gravitational field, the potential energy of every body will be zero. So, we will have energy at both points and solve for v′.
Formula used:
K.E=21mv2P.E=−RGMmve=R2GM
Complete step by step answer:
We will calculate the total energy of the ball at the surface of earth. Total energy will be equal to sum of kinetic and potential energy.
T.E=K.E+P.ET.E=21m(3ve)2+(−RGMm)
There, the velocity of the ball at earth's surface is given as 3ve, where ve is the escape velocity and it is given by the formula,
ve=R2GM
Where, G is the universal gravitational constant.
M is the mass of the earth.
R is the radius of the earth.
We will substitute this equation in the expression for total energy.
