Question

A ball is released from the top of a vertical circular pipe. Find angle $\theta$ vertically with the vertical where the ball will lose contact with the inner slide wall of the pipe and start moving with the outer side wall. (Thickness of the pipe is small compared to the radius of the circle.)
A) ${\cos ^{ - 1}}\dfrac{2}{3}$
B) ${\cos ^{ - 1}}\dfrac{1}{3}$
C) ${\sin ^{ - 1}}\dfrac{2}{3}$
D) ${\sin ^{ - 1}}\dfrac{1}{3}$

Answer 1

When a body moves in a circular path and is released then two forces are acting on the body at same time. If the body is in equilibrium then these forces are said to be in equilibrium.
For solving this question, we are going to place the two forces equally and after that we can easily apply conservation of energy if the rotating body is converted into kinetic energy.

Complete step by step solution:
When a body is moving in a vertical circular pipe, then two forces are acting on the body at same time. First is the centripetal force directed toward the centre of the vertical pipe and second force is the gravitational force which is acting normally downward.

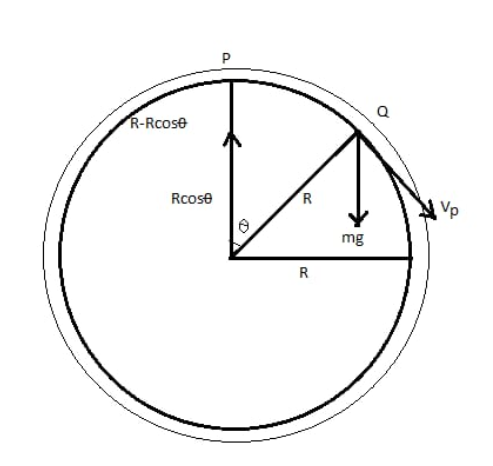
Now, consider the body is displaced at point $Q$ from point $P$ with velocity ${v_p}$. So at point $Q$ there are two force are acting simultaneously i.e.
Centripetal force$=$cosine component of $mg$
$\Rightarrow \dfrac{{m{v_p}^2}}{R} = mg\cos \theta$
$\Rightarrow {v_p}^2 = gR\cos \theta$ (i)
Here $m$ is the mass of the body and $\theta$ is the angle at which the body is in equilibrium at point $Q$.
Body displaced to point $Q$ from point $P$, it displaced a small distance $PM$ which is the displacement of body $= R - R\cos \theta$
If body is in motion, then according to the conservation of energy-
Potential energy$=$Kinetic energy
$mgh = \dfrac{1}{2}m{v_p}^2$
Here $h$ is the displacement of the body. So, putting the value of $h$ in this equation.
$\Rightarrow mg(R - R\cos \theta ) = \dfrac{1}{2}m{v_p}^2 \\\ \Rightarrow g(R - R\cos \theta ) = \dfrac{1}{2}{v_p}^2 \\\$
$\Rightarrow {v_p}^2 = 2g(R - R\cos \theta )$ (ii)
Now, we are going to compare both velocity which we obtain from equation (i) and equation (ii)

$$\Rightarrow gR\cos \theta = 2g(R - R\cos \theta ) \\\ \Rightarrow gR\cos \theta = 2gR - 2gR\cos \theta \\\ \Rightarrow gR\cos \theta + 2gR\cos \theta = 2gR \\\ \Rightarrow 3gR\cos \theta = 2gR \\\ \Rightarrow 3\cos \theta = 2 \\\ \Rightarrow \cos \theta = \dfrac{2}{3} \\\ \Rightarrow \theta = {\cos ^{ - 1}}\dfrac{2}{3} \\\$$

Hence, at angle ${\cos ^{ - 1}}\dfrac{2}{3}$ the ball leaves the internal surface of the pipe and starts moving in an upward direction.

Therefore, option (A) is correct.

Note: It should be remembered that centripetal force is equal to the cosine of angle of $mg$ but mostly $mg\sin \theta$ is taken as equal component which gives an incorrect solution and potential energy is considered to the displacement between points $P$ and $Q$, not in the total revolution.