Question

A ball is projected from point A with velocity $10{\text{ m}}{{\text{s}}^{ - 1}}$ perpendicular to the inclined plane as in the figure. The range of the ball on the incline is

A. $40/3{\text{ m}}$
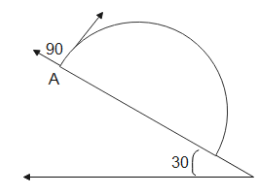
B. $20/13{\text{ m}}$
C. $13/20{\text{ m}}$
D. $40/3{\text{ m}}$

Answer 1

The projectile is perpendicular to the inclined plane with a certain velocity. Due to its acceleration due to gravity, the projectile forms a parabolic path. The projectile hits the end of the inclined plane of the parabolic path. We need to find the range of the projectile on the inclined plane.

Complete step by step answer:
The figure below shows the angle between the inclined plane and the horizontal is $30^\circ$. Let the angle be $\beta$ and the angle with which the projectile is thrown with the inclined plane is $\alpha = 60^\circ$. The projectile will thus hit the ground at some point at the bottom of the inclined plane. The distance covered by the projectile horizontally is called the range.

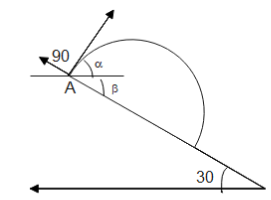
We know for a given projectile motion in an inclined plane, Range is given as
$R = \dfrac{{{u^2}}}{{g{{\cos }^2}\beta }}[\sin (2\alpha + \beta ) + \sin \beta ]$
Where $u = 10{\text{m}}{{\text{s}}^{ - 1}}$ is the initial velocity
Therefore substituting the values we get
$R = \dfrac{{{{10}^2}}}{{10{{\cos }^2}30}}[\sin (2 \times 60 + 30) + \sin 30]$
$\Rightarrow R = \dfrac{{10}}{{{{\cos }^2}30^\circ }}$
$\Rightarrow R = \dfrac{{40}}{3}$

Hence option A is the correct answer.

Additional information: Projectile motion on an inclined plane is one of the various projectile motion types. The main distinguishing aspect is that points of projection and return are not on the same horizontal plane. There are two possibilities: the point of return is at a higher level than the point of projection that is projectile is thrown up the incline and the point of return is at a lower level than the point of projection that is projectile is thrown down the incline.

Note: The angle between the velocity and the horizontal is calculated using the two angles given, that is the angle of the inclined plane with the horizontal and the perpendicular angle to the inclined plane at which the projectile was thrown. The angle of the projectile with the horizontal is not the angle of the velocity with the inclined plane.