Question

A ball is projected from a point on the floor with a speed of $15{\text{ m/s}}$ at an angle of ${60^ \circ }$ with the horizontal. Will it hit a vertical wall $5{\text{ m}}$ away from the point of projection and perpendicular to the plane of projection without hitting the floor? Will the answer differ if the wall is ${\text{22 m}}$ away?

Answer 1

In this question, a ball is projected, and we need to find out will it hit a vertical wall at a certain distance away from the point of projection. To solve this question, we need to find the range of the projectile. If the range of a projectile is greater than the distance of the wall from the point of projection, then the ball hits the wall else it will hit the floor first
Horizontal Range of a projectile, ${\text{R = }}\dfrac{{{{\text{u}}^2}\sin 2\theta }}{g}$
Where ${\text{u}}$ is the velocity of the projection
$\theta$ is the angle of projectile with the horizontal
$g = 9.8{\text{ m/}}{{\text{s}}^2}$ (Acceleration due to gravity).

Complete answer:
We are given,
The velocity of the projection of ball, ${\text{u}} = 15{\text{ m/s}}$
The angle of projection of the ball, $\theta = {60^ \circ }$

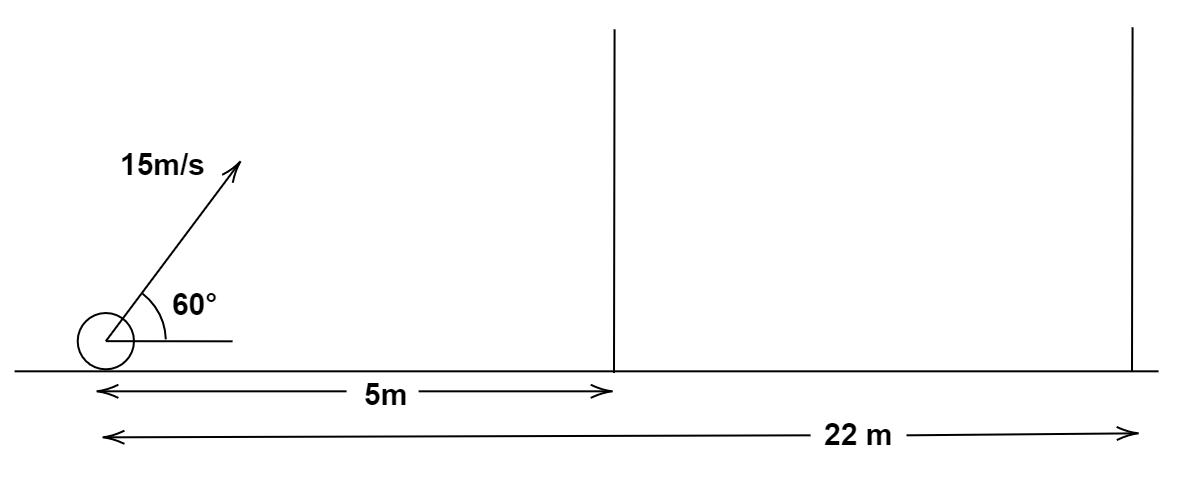
We need to find out if the ball hits the vertical wall at a distance of $5{\text{ m}}$ away from the point of projection.
If the range of the projectile is greater than $5{\text{ m}}$ then the projectile hits the wall else, it does not hit the wall.
Thus, we need to find out the range of the projectile of the ball
Range, ${\text{R = }}\dfrac{{{{\text{u}}^2}\sin 2\theta }}{g}$
Now substituting the values in the formula we get,
$R = \dfrac{{{{\left( {15} \right)}^2}\sin {{120}^ \circ }}}{{9.8}}$
Substituting $\sin {120^ \circ } = \dfrac{{\sqrt 3 }}{2}$
$\Rightarrow R = \dfrac{{225 \times \sqrt 3 }}{{2 \times 9.8}}$
On solving we get,
$R = 19.88{\text{ m}}$
As the range $R$ is greater than $5{\text{ m}}$ the ball will definitely hit the vertical wall
For the second part of the question,
The wall is placed at a distance of ${\text{22 m}}$ from the point of projection
Since the range of a projectile of ball, $R = 19.88{\text{ m}}$ is less than ${\text{22 m}}$ so the wall is not within the horizontal range of the ball
Hence, the ball will not hit the wall in the second case.

Note:
The horizontal range value is maximum if the angle of projection $\theta = {45^ \circ }$ and for the same value of initial velocity horizontal range of a projectile for complementary angle is same. The formula ${\text{R = }}\dfrac{{{{\text{u}}^2}\sin 2\theta }}{g}$ is only valid for the case when projectile is projected obliquely on the surface of the earth.