Question
Question: A ball is projected from a 20m high tower. Find the time taken and horizontal range to reach the gro...
A ball is projected from a 20m high tower. Find the time taken and horizontal range to reach the ground.
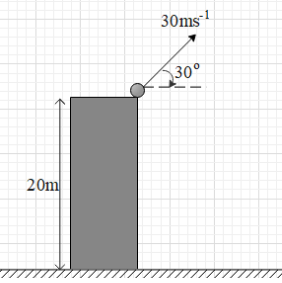
Solution
First calculate the initial vertical and initial horizontal velocities of the projectile. Then use suitable kinematic equations and calculate the time taken for the projectile to reach the ground and the horizontal range of the projectile.
Formula used:
ux=ucosθ
uy=usinθ
where ux is the initial horizontal velocity and uy is the initial vertical velocity of the projectile. u is the net initial velocity and θ is the angle of projection of the projectile.
s=uyt−21gt2
where s is the displacement of the projectile at time t and g is acceleration due to gravity.
R=uxT
where R is the horizontal range of the projectile and T is the time taken to reach the ground.
Complete step by step answer:
In the given figure, we can see that u=30ms−1 and θ=30∘.
Then this means that the initial horizontal velocity of the projectile is ux=ucosθ=30cos30∘=153ms−1
And the initial vertical velocity of the projectile is uy=usinθ=30sin30∘=15ms−1.
When the projectile comes down and strikes the ground, the vertical displacement of the projectile is s=−20m (as the height of the tower is 20m).
Now, let us use the kinematic equation s=uyt−21gt2.
In this case, uy=15ms−1, s=−20m and g=10ms−2.
Then,
⇒−20=15t−21(10)t2
⇒5t2−15t−20=0
⇒t2−3t−4=0
⇒(t−4)(t+1)=0
∴(t−4)=0 or (t−1)=0
Then means that either t=4s or t=−1s.
But we know that time cannot be a negative value.
Therefore, we consider t=4s
Then this means that T=t=4s.
Therefore, the time taken by the projectile to reach the ground is 4s.
With this, we get that R=uxT=153×4=603m.
Therefore, the horizontal range of the projectile is equal to 603m.
Note: In a projectile motion, the gravity pulls the projectile in the downward direction. As a result, the projectile only accelerates in the downward direction and its acceleration in the horizontal direction is zero.Hence, we can find the horizontal range just be using the distance formula, which d=vt, where d is distance travelled in a direction, v is its velocity in that direction and t is time.
