Question
Question: A ball is held at rest in position A in figure by two light cords. The horizontal cord is cut and th...
A ball is held at rest in position A in figure by two light cords. The horizontal cord is cut and the ball starts swinging as a pendulum. The ratio of the tension in the supporting cord in position B, to that in position A is
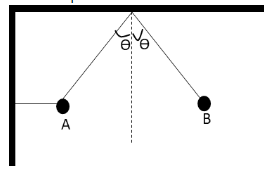
A. sin2θ
B. cos2θ
C. tan2θ
D. 1:1
Solution
Draw the free body diagram of the balls in position A and B. Use the expression for Newton’s second law of motion. Apply Newton’s second law of motion to the balls in at positions A and B and determine the values of tensions in the cords and then take the ratio of these tensions in the asked manner to calculate the final answer.
Formula used:
The expression for Newton’s second law of motion is
Fnet=ma
Here, Fnet is net force acting on the object, m is mass of the object and a is acceleration of the object.
Complete step by step answer:
Let m be the mass of the two balls. Let us draw the free body diagram of the two balls is as follows:

In the above free body diagram, mg is the weight of the two balls, TA is the tension in the cord holding the ball at position A and TB is the tension in the cord holding the ball at position B.
Let is apply Newton’s second law of motion to the ball at position A.
TAcosθ=mg
⇒TA=cosθmg
Let is apply Newton’s second law of motion to the ball at position B.
TB=mgcosθ
Now let us determine the ratio of the tensions in the cords.
⇒TATB=cosθmgmgcosθ
∴TATB=cos2θ
Therefore, the ratio of the tension in the cord in position B to that in position A is cos2θ.
Hence, the correct option is B.
Note: The students should be careful while drawing the free body diagram of eh balls at positions A and B. If this free body diagram is not drawn correctly with the correct directions and positions of all the forces then the expressions for the tensions in the cords will be incorrect and hence the final answer will also be incorrect.
