Question
Question: A ball is dropped vertically from a height \(d\) above the ground it hits the ground and bounces up ...
A ball is dropped vertically from a height d above the ground it hits the ground and bounces up vertically to a height 2d. Neglecting subsequent motion and air resistances, its velocity v varies with the height h above the ground as:
A.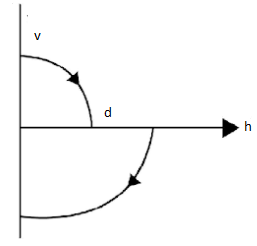
B.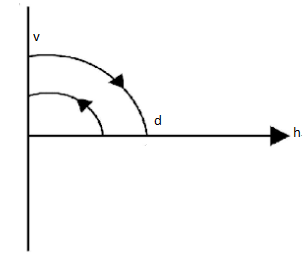
C.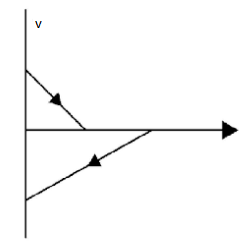
D.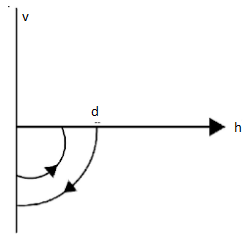
Solution
Here we have to use the third equation of motion to get the answer.
In physics, equations of motion are classified as equations that characterise a physical system’s behaviour in terms of its motion as a function of time. For deriving components such as displacement, velocity, time and acceleration, there are three motion equations that can be used.
The equations of motion can also be said as the equations of kinematics.
Complete step by step solution:
Let u be the initial velocity and v be the final velocity.
Let a be the acceleration and s be the distance.
Now we use the third equation of motion.
The third equation of motion gives the final velocity of an object under uniform acceleration given the distance travelled and an initial velocity.
The third equation of motion is especially used to find the distance.
The third equation of motion is given mathematically as:
v2−u2=2as
Since the initial velocity is zero.
So,
v2=2as
So, the graph is parabolic.
The velocity is going to be negative when the ball sinks while it is going to be positive as it bounces up i.e. they are going to get opposite direction, even the ultimate height will be 2d .
Hence, option A is correct.
Additional information:
During uniformly accelerated, straight-line motion, the relation between velocity and time is a clear one. The longer the acceleration, the greater the velocity variation. Velocity shift is strictly proportional to the time that continuous acceleration occurs. If velocity increases for a given time by a certain amount, twice the time, it can increase by twice the amount. If an object had already begun at a certain velocity, so the old velocity plus this adjustment would be its current velocity.
Note:
Here we have to take the initial velocity as zero since it is not provided in the question. So, while solving the question we have to see if initial velocity is provided or not and what is asked in the question.
