Question

A ball is dropped from the top of a building 25m high. How much time will the ball need to reach the ground?

Answer 1

As a first step, you could note down all the values that are directly and indirectly given in the question. Then you could make a rough sketch for better clarity of the situation. After that substitute all the given values in the appropriate equation of motion and thereby, you will get the answer.

Formula used:
Equation of motion,
$s=ut+\dfrac{1}{2}g{{t}^{2}}$

Complete Step by step solution:
In the question, we are told that a ball is being dropped from the top of a building of height 25m. We are asked to find the time taken by the ball to reach the ground.
So we are dealing with a kinematic problem, let us see what quantities are given in the question.

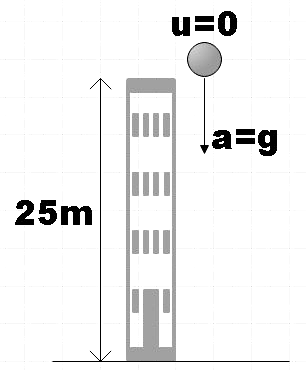
We are said that the ball is dropped from a certain height, so the initial velocity of the body would be zero, that is,
$u=0$
Also, we are given the height of the building as 25m. So, the distance covered by the ball in order to reach the ground is,
$s=25m$
As the ball is under free fall, the only force that would influence this motion will be that due to gravity. So the acceleration on the ball will be g, that is,
$a=g=10m{{s}^{-2}}$
Now let us recall Newton’s equation of motion which is given by,
$s=ut+\dfrac{1}{2}g{{t}^{2}}$
Substituting we get,
$25=0+\dfrac{1}{2}\left( 10 \right){{t}^{2}}$
$\Rightarrow {{t}^{2}}=\dfrac{50}{10}$
$\therefore t=\pm 5$

As the time cannot be negative, we could say that the ball takes $t=5s$ to reach the ground.

Note:
Though the value of acceleration due to gravity is not given in the question, we have taken its approximate value to be $10m{{s}^{-2}}$. Then, the first thing that we should take care of is the direction and hence the sign of different quantities. By convention, we say g is positive downwards and we have taken it to be so.